Câu 40 trang 74 SGK Hình học 11 Nâng cao

Trong các mệnh đề sau, mệnh đề nào đúng ?

a. Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau

b. Hình chiếu song song của hai đường thẳng chéo nhau thì cắt nhau

c. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau

d. Hình chiếu song song của hai đường thẳng chéo nhau có thể cắt nhau, trùng nhau, song song với nhau

Giải

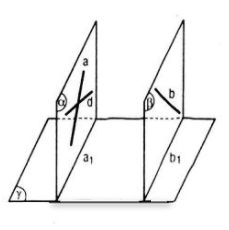
a) Sai vì nếu hình chiếu song song của hai đường thẳng mà trùng nhau thì hai đường thẳng đó cùng thuộc một mặt phẳng.

b) Sai vì hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.

c) Đúng.

d) Sai.

Câu 41 trang 74 SGK Hình học 11 Nâng cao

Trong các mệnh đề sau, mệnh đề nào đúng ?

a. Hình chiếu song song của hai đường thẳng cắt nhau có thể song song với nhau

b. Hình chiếu song song của hai đường thẳng cắt nhau có thể cắt nhau

c. Hình chiếu song song của hai đường thẳng cắt nhau có thể trùng nhau

d. Một đường thẳng có thể song song với hình chiếu song song của nó

e. Một đường thẳng luôn cắt hình chiếu song song của nó

f. Một đường thẳng có thể trùng với hình chiếu song song của nó

Giải

a) Sai

b) Đúng.

c) Đúng.

d) Đúng.

e) Sai.

f) Đúng.

Câu 42 trang 74 SGK Hình học 11 Nâng cao

Tam giác ABC có hình chiếu song song là tam giác A’B’C’. Chứng minh rằng trọng tâm tam giác ABC có hình chiếu song song là trọng tâm tam giác A’B’C’

Giải

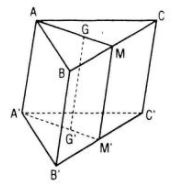
Gọi G là trọng tâm ∆ABC, M là trung điểm BC

G’, M’ là hình chiếu song song của G và M.

Ta có M’ là trung điểm B’C’ và \({{A'G'} \over {G'M'}} = {{AG} \over {GM}} = 2\)

\(⇒\) G’ là trọng tâm ∆A’B’C’.

Câu 43 trang 75 SGK Hình học 11 Nâng cao

Vẽ hình biểu diễn của một tứ diện và trọng tâm của nó

Giải

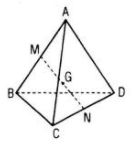
Hình biểu diễn của một tứ diện là tứ giác ABCD.

Lấy M và N lần lượt là trung điểm AB và CD thì trung điểm G của MN sẽ biểu diễn cho trọng tâm của tứ diện.

Câu 44 trang 75 SGK Hình học 11 Nâng cao

Vẽ hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn

Giải

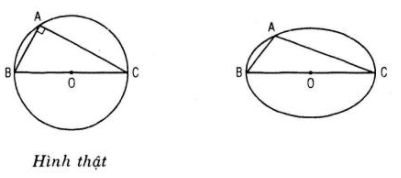
Vẽ elip tâm O là hình biểu diễn của đường tròn đã cho. Lấy B và C là hai điểm trên elip sao cho B, O, C thẳng hàng và một điểm A thuộc elip sao cho A khác B và C. Khi đó, tam giác ABC là hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn.

Câu 45 trang 75 SGK Hình học 11 Nâng cao

Vẽ hình biểu diễn của một hình vuông nội tiếp trong một đường tròn

Giải

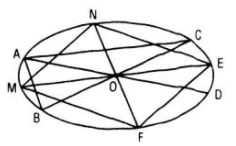
Theo bài 44, vẽ tam giác ABC là hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn. Qua O ta kẻ hai dây ME và NF của elip lần lượt song song với AC và AB. Khi đó tứ giác MNEF là hình biểu diễn của một hình vuông nội tiếp trong một đường tròn.

Câu 46 trang 75 SGK Hình học 11 Nâng cao

Vẽ hình biểu diễn của một lục giác đều

Giải

Xét hình lục giác đều ABCDEF, ta thấy:

Tứ giác OABC là hình thoi.

Các điểm D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua tâm O.

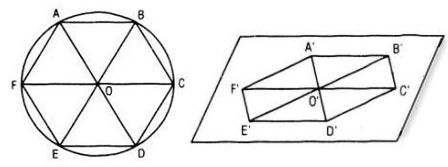
Từ đó ta suy ra cách vẽ hình biểu diễn của lục giác đều ABCDEF như sau:

- Vẽ hình bình hành O’A’B’C’ biểu diễn cho hình thoi OABC.

- Lấy các điểm D’, E’, F’ lần lượt đối xứng với các điểm A’, B’, C’ qua O’, ta được hình biểu diễn A’B’C’D’E’F’ của hình lục giác đều ABCDEF.

Câu 47 trang 75 SGK Hình học 11 Nâng cao

Cho hình hộp ABCD.A₁B₁C₁D₁. Tìm điểm I trên đường chéo B₁D và điểm J trên đường chéo AC sao cho IJ // BC₁. Tính tỉ số \({{ID} \over {I{B_1}}}\)

Giải

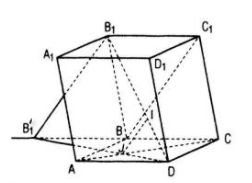
Giả sử, ta tìm được I ∈ B₁D, J ∈ AC sao cho  IJ // BC₁

Xét phép chiếu song song theo phương BC₁ lên mp(ABCD). Khi đó hình chiếu của các điểm I , D, B₁ lần lượt là J, D , B₁’

Do D, I ,B₁ thẳng hàng nên D, J, B₁’ thẳng hàng

Vậy J chính là giao điểm của hai đường thẳng B’₁D và AC. Từ đó ta có thể tìm I, J như sau:

- Dựng B’₁ là hình chiếu B₁ qua phép chiếu song song ở trên (BC₁B₁B’₁ là hình bình hành)

- Dựng J là giao điểm của B’₁D với AC

- Trong mp(B₁B’₁D) kẻ JI song song với B₁B’₁ cắt B₁D tại I

Rõ ràng I và J thỏa mãn điều kiện của bài toán

Dễ thấy B’₁ thuộc đường thẳng BC và \(AD = {1 \over 2}B{'_1}C\)

Từ đó suy ra : \({{ID} \over {I{B_1}}} = {{ID} \over {JB{'_1}}} = {{AD} \over {B{'_1}C}} = {1 \over 2}\)

Vậy ta có: \({{ID} \over {I{B_1}}} = {1 \over 2}\)

Giaibaitap.me