Câu 7 trang 95 SGK Hình học 11 Nâng cao

Mỗi khẳng định sau có đúng không ?

a. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau.

b. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì vuông góc với nhau.

Giải:

a. Sai : lấy hai đường thẳng cắt nhau b, c nằm trong mp(P) và a vuông góc với (P).

Khi đó, a ⊥ b, a ⊥ c nhưng b, c cắt nhau.

b. Sai : lấy b // c, b, c ⊂ (P) và a ⊥ (P)

Câu 8 trang 95 SGK Hình học 11 Nâng cao

a. Cho vecto \(\overrightarrow n \) khác \(\overrightarrow 0 \) và hai vecto \(\overrightarrow a ,\overrightarrow b \) không cùng phương. Chứng minh rằng nếu vecto \(\overrightarrow n \) vuông góc với cả hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) thì ba vecto \(\overrightarrow n ,\overrightarrow a ,\overrightarrow b \) không đồng phẳng.

b. Chứng minh rằng ba vecto cùng vuông góc với vecto \(\overrightarrow n  \ne \overrightarrow 0 \) thì đồng phẳng. Từ đó suy ra các đường thẳng cùng vuông góc với một đường thẳng thì cùng song song với một mặt phẳng.

Giải

a. Nếu \(\overrightarrow n ,\overrightarrow a ,\overrightarrow b \) đồng phẳng thì có hai số k, l sao cho \(\overrightarrow n  = k.\overrightarrow a  + l.\overrightarrow b \)

suy ra \(\overrightarrow n .\overrightarrow n  = k\overrightarrow a .\overrightarrow n  + l\overrightarrow b .\overrightarrow n  = 0 \Rightarrow {\left| {\overrightarrow n } \right|^2} = {\overrightarrow n ^2} = 0 \)

\(\Rightarrow \left| {\overrightarrow n } \right| = 0 \)

\(\Rightarrow \overrightarrow n  = \overrightarrow 0 \) (vô lí)

vậy \(\overrightarrow n ,\overrightarrow a ,\overrightarrow b \) không đồng phẳng

b. Giả sử ba vecto cùng vuông góc với \(\overrightarrow n \) là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)

Tức là \(\overrightarrow a .\overrightarrow n  = \overrightarrow b .\overrightarrow n  = \overrightarrow c .\overrightarrow n  = 0\)

Nếu \(\overrightarrow a \) và \(\overrightarrow b \) là hai vecto cùng phương thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng

Nếu \(\overrightarrow a  \) và \(\overrightarrow b \) là hai vecto không cùng phương thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow n \) là ba vecto không đồng phẳng (điều này suy ra từ câu a)

Khi đó \(\overrightarrow c  = x\overrightarrow a  + y\overrightarrow b  + z\overrightarrow n .\) Nhân vô hướng hai vế với \(\overrightarrow n ,\) ta có \(\overrightarrow c .\overrightarrow n  = x\overrightarrow a .\overrightarrow n  + y\overrightarrow b .\overrightarrow n  + z{\overrightarrow n ^2}\) suy ra \(z{\overrightarrow n ^2} = 0\,hay\,z = 0,\) tức là \(\overrightarrow c  = x\overrightarrow a  + y\overrightarrow b .\)

Vậy các vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng

Nếu ba đường thẳng d₁, d₂, d₃ cùng vuông góc với một đường thẳng thì do kết quả nêu trên, ta có ba vecto chỉ phương của ba đường thẳng d₁,d₂ ,d₃ đồng phẳng tức là ba đường thẳng d₁,d₂ ,d₃ cùng song song với một mặt phẳng.

Câu 9 trang 96 SGK Hình học 11 Nâng cao

Cho hình chóp S.ABC có SA = SB = SC và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Chứng minh rằng SA ⊥ BC, SB ⊥ AC, SC ⊥ AB.

Giải

Ta có:

\(\eqalign{  & \overrightarrow {SA} .\overrightarrow {BC}  = \overrightarrow {SA} .\left( {\overrightarrow {SC}  - \overrightarrow {SB} } \right) \cr&= \overrightarrow {SA} .\overrightarrow {SC}  - \overrightarrow {SA} .\overrightarrow {SB}   \cr  &  = SA.SC.\cos \widehat {ASC} - SA.SB.\cos \widehat {ASB} = 0 \cr} \)

Suy ra : SA  ⊥ BC

Tương tự : SB ⊥ AC và SC ⊥ AB

Câu 10 trang 96 SGK Hình học 11 Nâng cao

Cho hình tứ diện ABCD. Chứng minh rằng nếu \(\overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AC} .\overrightarrow {AD}  = \overrightarrow {AD} .\overrightarrow {AB} \) thì AB ⊥ CD, AC ⊥ BD, AD ⊥ BC. Điều ngược lại có đúng không ?

Giải

Ta có:

\(\eqalign{  & \overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AC} .\overrightarrow {AD}   \Leftrightarrow \overrightarrow {AC} .\left( {\overrightarrow {AD}  - \overrightarrow {AB} } \right) = 0  \cr  &  \Leftrightarrow \overrightarrow {AC} .\overrightarrow {BD}  = 0 \Leftrightarrow AC \bot BD \cr} \)

Tương tự :

\(\eqalign{  & \overrightarrow {AC} .\overrightarrow {AD}  = \overrightarrow {AD} .\overrightarrow {AB}  \Leftrightarrow AD \bot BC  \cr  & \overrightarrow {AD} .\overrightarrow {AB}  = \overrightarrow {AB} .\overrightarrow {AC}  \Leftrightarrow AB \bot CD \cr} \)

Như vậy, điều ngược lại cũng đúng.

Câu 11 trang 96 SGK Hình học 11 Nâng cao

Cho hình tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = 60^\circ ,\widehat {BAD} = 60^\circ .\)

Chứng minh rằng :

a. AB ⊥ CD;

b. Nếu I và J lần lượt là trung điểm của AB và CD thì \(IJ \bot AB\) và \(IJ \bot CD.\)

Giải

a. Ta có:

\(\eqalign{  & \overrightarrow {AB} .\overrightarrow {CD}  = \overrightarrow {AB} .\left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AC}   \cr  &  = AB.AD.\cos \widehat {BAD} - AB.AC.\cos \widehat {BAC} = 0  \cr  &  \Rightarrow AB \bot CD. \cr} \)

b.

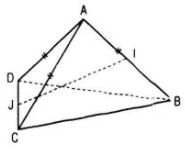
Ta có:

\(\eqalign{  & \overrightarrow {IJ}  = \overrightarrow {IA}  + \overrightarrow {AJ}   \cr  &  = {1 \over 2}\overrightarrow {BA}  + {1 \over 2}\left( {\overrightarrow {AD}  + \overrightarrow {AC} } \right)  \cr  &  = {1 \over 2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right)  \cr  &  = {1 \over 2}\left( {\overrightarrow {AD}  + \overrightarrow {AC}  - \overrightarrow {AB} } \right) \cr} \)

Suy ra :

\(\eqalign{  & \overrightarrow {AB} .\overrightarrow {IJ}  = {1 \over 2}\left( {\overrightarrow {AB} .\overrightarrow {AD}  + \overrightarrow {AB} .\overrightarrow {AC}  - A{B^2}} \right)  \cr  &  ={1 \over 2} \left( {AB.AD.\cos 60^\circ } + AB.AC.\cos 60^\circ  - A{B^2} \right) \cr&= 0  \cr  &  \Rightarrow AB \bot IJ \cr} \)

Mặt khác :

\(\eqalign{  & \overrightarrow {CD} .\overrightarrow {IJ}  = {1 \over 2}\left( {\overrightarrow {CA}  + \overrightarrow {AD} } \right).\left( {\overrightarrow {AD}  + \overrightarrow {BA}  + \overrightarrow {AC} } \right)  \cr  &  = {1 \over 2}\left( { - \overrightarrow {AC} .\overrightarrow {AD}  + {{\overrightarrow {AD} }^2} + \overrightarrow {CA} .\overrightarrow {BA}  + \overrightarrow {AD} .\overrightarrow {BA}  - {{\overrightarrow {AC} }^2} + \overrightarrow {AD} .\overrightarrow {AC} } \right)  \cr  &  =  - {1 \over 2}\overrightarrow {AB} .\left( {\overrightarrow {CA}  + \overrightarrow {AD} } \right) =  - {1 \over 2}\overrightarrow {AB} .\overrightarrow {CD}  = 0  \cr  &  \Rightarrow CD \bot IJ \cr} \)

Giaibaitap.me