Câu 1 trang 223 SGK Đại số và Giải tích 11 Nâng cao

a. Tính \(\sin {\pi  \over 8}\,\text{ và }\,\cos {\pi  \over 8}\)

b. Chứng minh rằng có hằng số C > 0 để có đẳng thức

\(\sin x + \left( {\sqrt 2  - 1} \right)\cos x = C\cos \left( {x - {{3\pi } \over 8}} \right)\) với mọi x.

Giải:

a. Ta có:

\(\eqalign{  & {\sin ^2}{\pi  \over 8} = {{1 - \cos {\pi  \over 4}} \over 2} = {{1 - {{\sqrt 2 } \over 2}} \over 2} = {{2 - \sqrt 2 } \over 4}  \cr  &  \Rightarrow \sin {\pi  \over 8} = {1 \over 2}\sqrt {2 - \sqrt 2 }   \cr  & {\cos ^2}{\pi  \over 8} = {{1 + \cos {\pi  \over 4}} \over 2} = {{1 + {{\sqrt 2 } \over 2}} \over 2} = {{2 + \sqrt 2 } \over 4}  \cr  &  \Rightarrow \cos {\pi  \over 8} = {1 \over 2}\sqrt {2 + \sqrt 2 }  \cr} \)

b. Ta có:

\(\eqalign{  & {1^2} + {\left( {\sqrt 2  - 1} \right)^2} = 4 - 2\sqrt 2 .\,\text{ Do đó}\,:  \cr  & \sin x + \left( {\sqrt 2  - 1} \right)\cos x  \cr  &  = \left( {\sqrt {4 - 2\sqrt 2 } } \right)\left( {{1 \over {\sqrt {4 - 2\sqrt 2 } }}\sin x + {{\sqrt 2  - 1} \over {\sqrt {4 - 2\sqrt 2 } }}\cos x} \right)  \cr  &  = \sqrt {4 - 2\sqrt 2 } \left( {\sin x\cos {\pi  \over 8} + \sin {\pi  \over 8}\cos x} \right)  \cr  &  = \sqrt {4 - 2\sqrt 2 } \sin \left( {x + {\pi  \over 8}} \right)  \cr  &  = \sqrt {4 - 2\sqrt 2 } \cos \left( {x - {{3\pi } \over 8}} \right)  \cr  & \text{ Vì }\,{1 \over {\sqrt {4 - 2\sqrt 2 } }} = {{\sqrt {4 + 2\sqrt 2 } } \over {\sqrt 8 }} = {1 \over 2}\sqrt {2 + \sqrt 2 }  = \cos {\pi  \over 8}.  \cr  & \text{Vậy }\,C = \sqrt {4 - 2\sqrt 2 }  \cr} \)

Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao

Giải phương trình

\(\tan x = \cot 2x\)

Biểu diễn các nghiệm trên đường tròn lượng giác.

Giải:

Điều kiện

\({\mathop{\rm cosx}\nolimits} .sin2x \ne 0 \Leftrightarrow \left\{ {\matrix{   {\sin x \ne 0}  \cr   {\cos x \ne 0}  \cr  } } \right. \Leftrightarrow x \ne k{\pi  \over 2}\)

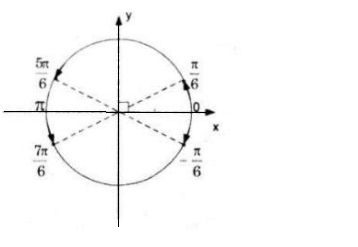
\(\eqalign{  & \tan x = \cot 2x \Leftrightarrow {{\sin x} \over {\cos x}} = {{\cos 2x} \over {\sin 2x}} \cr& \Leftrightarrow\cos x \cos 2x - \sin x\sin 2x = 0  \cr  &  \Leftrightarrow \cos 3x = 0 \Leftrightarrow \cos x\left( {4{{\cos }^2}x - 3} \right) = 0  \cr  &  \Leftrightarrow {\cos ^2}x = {3 \over 4}  \cr  &  \Leftrightarrow {{1 + \cos 2x} \over 2} = {3 \over 4} \Leftrightarrow \cos 2x = {1 \over 2}  \cr  &  \Leftrightarrow x =\pm {\pi  \over 6} + k\pi  (k\in\mathbb Z) \cr} \)

Biểu diễn nghiệm trên đường tròn được 4 điểm.

Câu 3 trang 223 SGK Đại số và Giải tích 11 Nâng cao

a. Tìm giá trị nhỏ nhất của biểu thức \(P\left( x \right) = {\left( {\sin x + \cos x} \right)^3}\)

b. Tìm giá trị nhỏ nhất của biểu thức \(Q\left( x \right) = {1 \over {{{\sin }^2}x{{\cos }^2}x}}\)

c. Tìm giá trị nhỏ nhất của biểu thức \(R\left( x \right) = P\left( x \right) + Q\left( x \right)\)

Giải:

a. \(P\left( x \right) = 2\sqrt 2 {\cos ^3}\left( {x - {\pi  \over 4}} \right) \ge  - 2\sqrt 2 \) (đẳng thức xảy ra khi \(x =  - {{3\pi } \over 4}+k2\pi\) )

Vậy \(\min P\left( x \right) =  - 2\sqrt 2 \)

b. \(Q\left( x \right) = {4 \over {{{\sin }^2}2x}} \ge 4\) (đẳng thức xảy ra, chẳng hạn khi \(x =  \pm {{3\pi } \over 4}\) )

Vậy min Q(x) = 4

c. \(R\left( x \right) = P\left( x \right) + Q\left( x \right) \ge 4 - 2\sqrt 2 \) (đẳng thức xảy ra, chẳng hạn khi \(x =  - {{3\pi } \over 4}\)

Vậy \({\mathop{\rm min\,R}\nolimits} \left( x \right) = 4 - 2\sqrt 2 \)

Câu 4 trang 223 SGK Đại số và Giải tích 11 Nâng cao

Giải các phương trình :

a. \({\sin ^4}x + {\cos ^4}x = {3 \over 4}\)

b. \({\sin ^2}2x - {\sin ^2}x = {\sin ^2}{\pi  \over 4}\)

c. \(\cos x\cos 2x = \cos 3x\)

d. \(\tan 2x - \sin 2x + \cos 2x - 1 = 0\)

Giải:

a.

\(\eqalign{  & {\sin ^4}x + {\cos ^4}x = {3 \over 4}  \cr  &  \Leftrightarrow 1 - 2{\sin ^2}x{\cos ^2}x = {3 \over 4}  \cr  &  \Leftrightarrow 1 - {1 \over 2}{\sin ^2}2x = {3 \over 4}  \cr  &  \Leftrightarrow {\sin ^2}2x = {1 \over 2} \Leftrightarrow {{1 - \cos 4x} \over 2} = {1 \over 2}  \cr  &  \Leftrightarrow \cos 4x = 0 \Leftrightarrow x = {\pi  \over 8} + k{\pi  \over 4},k \in\mathbb Z \cr} \)

b.

\(\eqalign{  & {\sin ^2}2x - {\sin ^2}x = {\sin ^2}{\pi  \over 4}  \cr  &  \Leftrightarrow 4{\sin ^2}x{\cos ^2}x - {\sin ^2}x = {1 \over 2}  \cr  &  \Leftrightarrow 8{\sin ^2}x\left( {1 - {{\sin }^2}x} \right) - 2{\sin ^2}x = 1  \cr  &  \Leftrightarrow 8{\sin ^4}x - 6{\sin ^2}x + 1 = 0  \cr  &  \Leftrightarrow \left[ {\matrix{   {{{\sin }^2}x = {1 \over 2}}  \cr   {{{\sin }^2}x = {1 \over 4}}  \cr  } } \right. \Leftrightarrow \left[ {\matrix{   {{{1 - \cos 2x} \over 2} = {1 \over 2}}  \cr   {{{1 - \cos 2x} \over 2} = {1 \over 4}}  \cr  } } \right.  \cr  &  \Leftrightarrow \left[ {\matrix{   {\cos 2x = 0}  \cr   {\cos 2x = {1 \over 2}}  \cr  } } \right. \Leftrightarrow \left[ {\matrix{   {x = {\pi  \over 4} + k{\pi  \over 2}}  \cr   {x = {\pi  \over 6} + k{\pi  \over 2}}  \cr  } } \right. \cr} \)

c.

\(\eqalign{  & \cos x\cos 2x = \cos 3x  \cr  &  \Leftrightarrow {1 \over 2}\left( {\cos 3x + \cos x} \right) = \cos 3x  \cr  &  \Leftrightarrow \cos 3x = \cos x  \cr  &  \Leftrightarrow \left[ {\matrix{   {3x = x + k2\pi }  \cr   {3x =  - x + k2\pi }  \cr  } } \right. \Leftrightarrow \left[ {\matrix{   {x = k\pi }  \cr   {x = k{\pi  \over 2}}  \cr  } } \right.\cr& \Leftrightarrow x = k{\pi  \over 2},k \in\mathbb Z \cr} \)

d. Điều kiên: \(\cos 2x \ne0\)

\(\eqalign{  & \tan 2x - \sin 2x + \cos 2x - 1 = 0  \cr  &  \Leftrightarrow \tan 2x\left( {1 - \cos 2x} \right) - \left( {1 - \cos 2x} \right) = 0  \cr  &  \Leftrightarrow \left( {1 - \cos 2x} \right)\left( {\tan 2x - 1} \right) = 0  \cr  &  \Leftrightarrow \left[ {\matrix{   {\tan 2x = 1}  \cr   {\cos 2x = 1}  \cr  } } \right. \Leftrightarrow \left[ {\matrix{   {x = {\pi  \over 8} + k{\pi  \over 2}}  \cr   {x = k\pi }  \cr  } } \right. k \in\mathbb Z  \cr} \)

Câu 5 trang 224 SGK Đại số và Giải tích 11 Nâng cao

Giải các phương trình sau :

a. \(2\sin \left( {x + 10^\circ } \right) - \sqrt {12} \cos \left( {x + 10^\circ } \right) = 3\)

b. \(\sqrt 3 \cos 5x + \sin 5x = 2\cos 3x\)

c. \({\sin ^2}x - 3\sin x\cos x + 2{\cos ^2}x = 0\)

Giải

a.

\({a^2} + {b^2} = {2^2} + {\left( { - \sqrt {12} } \right)^2} = 16.\) Chia hai vế cho \(\sqrt {{a^2} + {b^2}}  = 4\) ta được :

\(\eqalign{  & {1 \over 2}\sin \left( {x + 10^\circ } \right) - {{\sqrt 3 } \over 2}\cos \left( {x + 10^\circ } \right) = {3 \over 4}  \cr  &  \Leftrightarrow \sin \left( {x + 10^\circ } \right)\cos 60^\circ  - \sin 60^\circ \cos \left( {x + 10^\circ } \right) = {3 \over 4}  \cr  &  \Leftrightarrow \sin \left( {x - 50^\circ } \right) = \sin \alpha \,\text{ với }\,\sin \alpha  = {3 \over 4}  \cr  &  \Leftrightarrow \left[ {\matrix{   {x - 50^\circ  = \alpha  + k360^\circ }  \cr   {x - 50^\circ  = 180^\circ  - \alpha  + k360^\circ }  \cr  } } \right.  \cr  &  \Leftrightarrow \left[ {\matrix{   {x = \alpha  + 50^\circ  + k360^\circ }  \cr   {x = 230^\circ  - \alpha  + k360^\circ }  \cr  } } \right. \cr} \)

b.

\(\eqalign{  & \sqrt 3 \cos 5x + \sin 5x = 2\cos 3x  \cr  &  \Leftrightarrow {{\sqrt 3 } \over 2}\cos 5x + {1 \over 2}\sin 5x = \cos 3x  \cr  &  \Leftrightarrow \cos 5x.\cos {\pi  \over 6} + \sin 5x\sin {\pi  \over 6} = \cos 3x  \cr  &  \Leftrightarrow \cos \left( {5x - {\pi  \over 6}} \right) = \cos 3x  \cr  &  \Leftrightarrow \left[ {\matrix{   {5x - {\pi  \over 6} = 3x + k2\pi }  \cr   {5x - {\pi  \over 6} =  - 3x + k2\pi }  \cr  } } \right. \Leftrightarrow \left[ {\matrix{   {x = {\pi  \over {12}} + k\pi }  \cr   {x = {\pi  \over {48}} + k{\pi  \over 4}}  \cr  } } \right. \cr} \)

c. * \(\cos x = 0 \Rightarrow \sin x =  \pm 1\,\text{ nên }\,x = {\pi  \over 2} + k\pi \) không là nghiệm của phương trình.

* Chia hai vế phương trình cho \({\cos ^2}x\) ta được :

\({\tan ^2}x - 3\tan x + 2 = 0 \Leftrightarrow \left[ {\matrix{   {\tan x = 1}  \cr   {\tan x = 2}  \cr  } } \right.\)

\(\Leftrightarrow \left[ {\matrix{   {x = {\pi  \over 4} + k\pi }  \cr   {x = \arctan 2 + k\pi }  \cr  } } \right.\)

 Giaibaitap.me