Bài 2.49 trang 86 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B’, C’, D’ sao cho đường thẳng B’C’cắt đường thẳng BC tại K, đường thẳng C’D’ cắt đường thẳng CD tại J, đường thẳng D’B’ cắt đường thẳng DB tại I.
a) Chứng minh ba điểm I, J, K thẳng hàng.
b) Lấy điểm M ở giữa đoạn thẳng BD; điểm N ở giữa đoạn thẳng CD sao cho đường thẳng MN cắt đường thẳng BC và điểm F nằm bên trong tam giác ABC. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (MNF).
Giải:
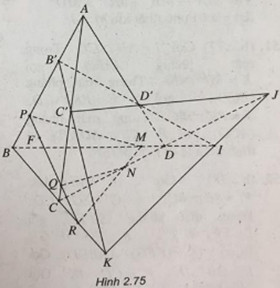
(h.2.75) a) Chú ý rằng I, J, K thẳng hàng vì chúng cùng thuộc giao tuyến của hai mặt phẳng (CBD) và (C’B’D’)
b) 4. Vì 4 điểm không đồng phẳng sẽ tạo nên 1 tứ diện => có 4 mặt
Bài 2.50 trang 87 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Tìm vị trí điểm M trong không gian sao cho:
\(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị cực tiểu.
Giải:
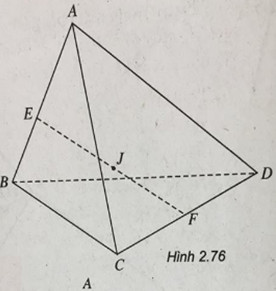
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
\(M{A^2} + M{B^2} = 2M{E^2} + {1 \over 2}A{B^2}\,\,\,\,\,\left( 1 \right)\)
\(M{C^2} + M{D^2} = 2M{F^2} + {1 \over 2}C{{\rm{D}}^2}\,\,\,\,\,\left( 2 \right)\)
Cộng (1) và (2) ta có:
\(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\)
\( = 2\left( {M{E^2} + M{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}\,\,} \right)\,\,\)
Gọi J là trung điểm của EF, ta có:
\(\left( {M{E^2} + M{F^2}} \right) = 2M{J^2}\, + {1 \over 2}E{F^2}\)
Khi đó:
\(\eqalign{
& M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2} \cr
& = 2\left( {2M{J^2}\, + {1 \over 2}E{F^2}} \right) + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr
& \ge E{F^2} + {1 \over 2}\left( {A{B^2} + C{{\rm{D}}^2}} \right) \cr} \)
Vậy \(M{A^2} + M{B^2} + M{C^2} + M{{\rm{D}}^2}\) đạt giá trị nhỏ nhất khi \(M \equiv J\).
Bài 2.51 trang 87 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Lấy điểm M thuộc đoạn AB. Gọi N, P là các điểm thuộc miền trong các tam giác ACD, BCD tương ứng. Xác định thiết diện tạo bởi mặt phẳng (MNP) cắt tứ diện ABCD.
Giải:
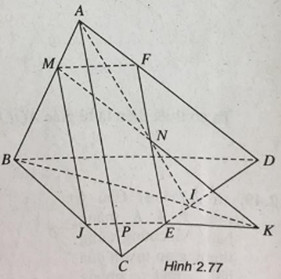
(h.2.77) Gọi \(I = AN \cap CD\). Trong mặt phẳng (ABI), gọi \(K = MN \cap BI\). Trong mặt phẳng (BCD), gọi \(E = PK \cap CD,J = PK \cap BC\). Trong mặt phẳng (ACD), gọi \(F = EN \cap A{\rm{D}}\). Ta có thiết diện là tứ giác MJEF.
Giaibaitap.me
Giải bài tập trang 87 bài đề toán tổng hợp Sách bài tập (SBT) Hình học 11. Câu 2.52: Cho hình chóp S.ABCD. Gọi E, F, G lần lượt là các điểm thuộc miền trong các tam giác SAB, SBC, SCD...
Giải đề toán trang 87 bài đề kiểm tra hình học chương 2 Sách bài tập (SBT) Hình học 11. Câu 1: Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)...
Giải đề toán 2 trang 88 bài đề kiểm tra toán hình học chương 2 Sách bài tập (SBT) Hình học 11. Câu 1: Chứng minh rằng (P) luôn chứa một đường thẳng cố định khi M thay đổi...
Giải đề toán 3 trang 88 bài kiểm tra hình học chương 2 Sách bài tập (SBT) Hình học 11. Câu 1: Cho tứ diện ABCD và M là điểm bất kì thuộc miền trong của tam giác BCD. Qua M kẻ các tia song song với AB, AC, AD...
