Cho tứ diện ABCD và M là điểm bất kì thuộc miền trong của tam giác BCD. Qua M kẻ các tia song song với AB, AC, AD. Các tia này theo thứ tự cắt các mặt (ACD), (ABD), (ABC) lần lượt tại B’, C’, D’
Câu 1. ( 3 điểm)
Xác định các giao điểm B’, C’, D’
Câu 2. ( 3 điểm)
Chứng minh \({{MB'} \over {AB}} + {{MC'} \over {AC}} + {{M{\rm{D}}'} \over {A{\rm{D}}}} = 1\)
Câu 3. ( 4 điểm)
Tìm giá trị lớn nhất của biểu thức \({{MB'} \over {AB}}.{{MC'} \over {AC}}.{{M{\rm{D}}'} \over {A{\rm{D}}}}\)
Giải:
Câu 1.
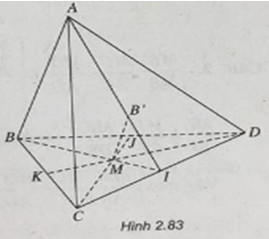
(h.2.83) \(\left( {ABM} \right) \cap \left( {BC{\rm{D}}} \right) = BM\)
Gọi I, J, K lần lượt là giao điểm của BM và CD; CM và BD; DM và BC.
Ta có : \(\left( {ABM} \right) \cap \left( {AC{\rm{D}}} \right) = AI\). Trong mặt phẳng (ABM), kẻ \(MB'\parallel AB\) với \(B' = MB' \cap AI\).
Ta có: \(B' = MB' \cap \left( {AC{\rm{D}}} \right)\)
Các điểm C’ và D’ được xác định tương tự.
Câu 2.
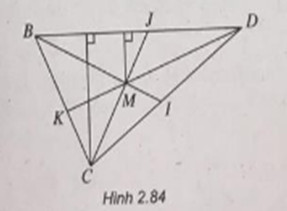
(h.2.84) Trong tam giác ABI, ta có:
\({{MB'} \over {AB}} = {{MI} \over {BI}}\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Tương tự ta cũng có:
\({{MC'} \over {AC}} = {{MJ} \over {CJ}}\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
\({{MD'} \over {AD}} = {{MK} \over {DK}}\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Cộng (1), (2), (3) lại ta có:
\({{MB'} \over {AB}} + {{MC'} \over {AC}} + {{M{\rm{D}}'} \over {A{\rm{D}}}} = {{MI} \over {BI}} + {{MJ} \over {CJ}} + {{MK} \over {DK}}\)
Ta chứng minh:
\({{MI} \over {BI}} + {{MJ} \over {CJ}} + {{MK} \over {DK}} = 1\)
Dễ thấy rằng :
\({{{S_{MB{\rm{D}}}}} \over {{S_{CB{\rm{D}}}}}} = {{{1 \over 2}B{\rm{D}}.d\left( {M,B{\rm{D}}} \right)} \over {{1 \over 2}B{\rm{D}}{\rm{.d}}\left( {C,B{\rm{D}}} \right)}} = {{MJ} \over {CJ}}\)
Tương tự
\({{{S_{MC{\rm{D}}}}} \over {{S_{{\rm{BCD}}}}}} = {{MI} \over {BI}}\), \({{{S_{MBC}}} \over {{S_{DBC}}}} = {{MK} \over {DK}}\)
Như vậy:
\({{MI} \over {BI}} + {{MJ} \over {CJ}} + {{MK} \over {DK}} = {{{S_{MC{\rm{D}}}} + {S_{MB{\rm{D}}}} + {S_{MBC}}} \over {{S_{BC{\rm{D}}}}}} = {{{S_{BC{\rm{D}}}}} \over {{S_{BC{\rm{D}}}}}} = 1\)
Câu 3.
\({{MB'} \over {AB}} + {{MC'} \over {AC}} + {{MD'} \over {A{\rm{D}}}} \le {\left( {{{{{MI} \over {BI}} + {{MJ} \over {CJ}} + {{MK} \over {DK}}} \over 3}} \right)^3} = {1 \over 9}\). Dấu bằng xảy ra khi \({{MI} \over {BI}} = {{MJ} \over {CJ}} = {{MK} \over {DK}} = {1 \over 3}\), chẳng hạn khi M là trọng tâm.
Vậy \(\max \left( {{{MB'} \over {AB}}.{{MC'} \over {AC}}.{{MD'} \over {A{\rm{D}}}}} \right) = {1 \over 9}\)
Giaibaitap.me
Giải bài tập trang 131 bài 1 vecto trong không gian Sách bài tập (SBT) Hình học 11. Câu 3.1: Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’....
Giải bài tập trang 132 bài 1 Vecto trong không gian Sách bài tập (SBT) Hình học 11. Câu 3.4: Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a...
Giải bài tập trang 140 bài 2 hai đường thẳng vuông góc Sách bài tập (SBT) Hình học 11. Câu 3.8: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng...
Giải bài tập trang 141 bài 2 hai đường thẳng vuông góc Sách bài tập (SBT) Hình học 11. Câu 3.12: Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thằng song song thì vuông góc với đường thẳng kia....
