Bài 3.30 trang 153 Sách bài tập (SBT) Hình học 11

Tứ diện SABC có ba đỉnh A, B, C tạo thành tam giác vuông cân đỉnh  B và , có cạnh SA vuông góc với mặt phẳng (ABC) và SA = a.

a) Chứng minh mặt phẳng (SAB) vuông góc với  mặt phẳng (SBC).

b) Trong mặt phẳng (SAB) vẽ AH vuông góc với SB tại H, chứng minh \(AH \bot \left( {SBC} \right)\)

c) Tính độ dài đoạn AH.

d) Từ trung điểm O của đoạn AC vẽ OK vuông góc với (SBC) cắt (SBC) tại K. Tính độ dài đoạn OK.

Giải:

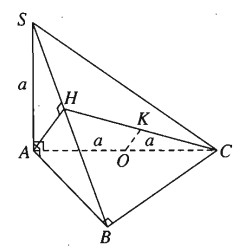
a)

\(\left. \matrix{
BC \bot AB \hfill \cr
BC \bot SA \hfill \cr} \right\} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)

b) \(AH \bot SB\) mà SB giao tuyến của hai  mặt phẳng vuông góc là (SBC) và (SAB) nên \(AH \bot \left( {SBC} \right)\).

c) Xét tam giác vuông SAB với đường cao AH  ta có:

\({1 \over {A{H^2}}} = {1 \over {A{S^2}}} + {1 \over {A{B^2}}} = {1 \over {{a^2}}} + {1 \over {2{a^2}}} = {3 \over {2{a^2}}}\)

Vậy \(AH = {{a\sqrt 6 } \over 3}\)

d) Vì \(OK \bot \left( {SBC} \right)\) mà \(AH \bot \left( {SBC} \right)\) nên \(OK\parallel AH\), ta có K thuộc CH.

\(OK = {{AH} \over 2} = {{a\sqrt 6 } \over 6}\).

Bài 3.31 trang 153 Sách bài tập (SBT) Hình học 11

Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử \(\left( \alpha  \right)\) là mặt phẳng đi qua A và vuông góc với cạnh SC, \(\left( \alpha  \right)\) cắt SC tại I.

a) Xác định giao điểm K của SO với mặt phẳng \(\left( \alpha  \right)\).

b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và \(B{\rm{D}}\parallel \left( \alpha  \right)\).

c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng \(\left( \alpha  \right)\). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng \(\left( \alpha  \right)\).

Giải:

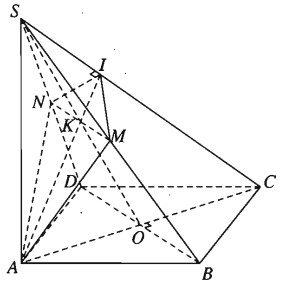
a) Gọi I là giao điểm của mặt phẳng \(\left( \alpha  \right)\) với cạnh SC. Ta có \(\left( \alpha  \right) \bot SC,AI \subset \left( \alpha  \right) \Rightarrow SC \bot AI\). Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và \(AI \subset \left( \alpha  \right)\), nên K là giao điểm của SO với \(\left( \alpha  \right)\).

b) Ta có

\(\left. \matrix{
B{\rm{D}} \bot AC \hfill \cr
B{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\) 

\( \Rightarrow B{\rm{D}} \bot SC\)

Mặt khác \(B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\) nên \(\left( {SB{\rm{D}}} \right) \bot \left( {SAC} \right)\).

Vì \(B{\rm{D}} \bot SC\) và \(\left( \alpha  \right) \bot SC\) nhưng BD không chứa trong \(\left( \alpha  \right)\) nên \(B{\rm{D}}\parallel \left( \alpha  \right)\)

Ta có \(K = SO \cap \left( \alpha  \right)\) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của \(\left( \alpha  \right)\) và (SBD). Mặt phẳng (SBD) chứa \(B{\rm{D}}\parallel \left( \alpha  \right)\) nên cắt  theo giao tuyến \(d\parallel B{\rm{D}}\). Giao tuyến này đi qua K là điểm chung của \(\left( \alpha  \right)\) và (SBD). Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

Bài 3.32 trang 154 Sách bài tập (SBT) Hình học 11

Hình chóp S.ABCD có đáy là hình thang svuông ABCD vuông tại A và D, có \(AB = 2{\rm{a}},A{\rm{D}} = DC = a\), có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.

a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).

b) Gọi \(\varphi \) là góc giữa hai mặt phẳng (SBC) và (ABCD), tính \(\tan \varphi \).

c) Gọi \(\left( \alpha  \right)\) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định \(\left( \alpha  \right)\) và xác định thiết diện của hình chóp S.ABCD với \(\left( \alpha  \right)\)

Giải:

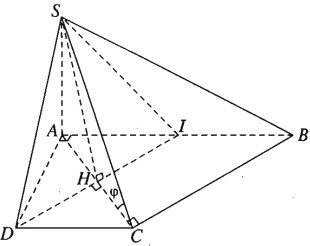
a) Ta có:

\(\left. \matrix{
C{\rm{D}} \bot A{\rm{D}} \hfill \cr
C{\rm{D}} \bot SA \hfill \cr} \right\} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\)

\( \Rightarrow \left( {SC{\rm{D}}} \right) \bot \left( {SA{\rm{D}}} \right)\)

Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì \(DI\parallel CB\) và \(DI \bot CA\) nên \(AC \bot CB\). Do đó \(CB \bot \left( {SAC} \right)\).

Vậy \(\left( {SBC} \right) \bot \left( {SAC} \right)\).

b) Ta có:

\(\varphi  = \widehat {SCA} \Rightarrow \tan \varphi  = {{SA} \over {AC}} = {a \over {a\sqrt 2 }} = {{\sqrt 2 } \over 2}\)

c)

\(\left. \matrix{
DI \bot AC \hfill \cr
DI \bot SA \hfill \cr} \right\} \Rightarrow DI \bot \left( {SAC} \right)\)

Vậy \(\left( \alpha  \right)\) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của \(\left( \alpha  \right)\) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng \(a\sqrt 2 \). Gọi H là tâm hình vuông AICD ta có \(SH \bot DI\) và \(SH = {{DI\sqrt 3 } \over 2} = {{a\sqrt 6 } \over 2}\). Tam giác SDI có diện tích:

\(\Delta S{\rm{D}}I = {1 \over 2}SH.DI = {1 \over 2}{{a\sqrt 6 } \over 2}.a\sqrt 2  = {{{a^2}\sqrt 3 } \over 2}\)

Giaibaitap.me