Câu 28 trang 160 Sách bài tập (SBT) Toán 8 tập 1

Tính diện tích của hình 186 theo các kích thước đã cho trên hình (a, b, c có cùng đơn vị đo).

Giải:                                                                 

Diện tích phần là hình chữ nhật :

S₁ = bc (đvdt)

Diện tích phần hình tam giác:

\({S_2} = {1 \over 2}c.\left( {a - b} \right)\) (đvdt)

Diện tích hình vẽ đó:

\(S = bc + {c \over 2}\left( {a - b} \right)\) (đvdt)

Câu 29 trang 160 Sách bài tập (SBT) Toán 8 tập 1

Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:

a. 10 \(c{m^2}\)

b. 15 \(c{m^2}\)

c. 20 \(c{m^2}\)

Giải:

Giả sử hai cạnh của tam giác là 5cm và 6cm. Chiều cao tương ứng của hai tam giác là h và k.

\({S_1} = {1 \over 2}.5.h;{S_2} = {1 \over 2}.6.k\)

h và k là đường cao ứng với cạnh đáy là 5 và 6. Theo tính chất của đường vuông góc và đường xiên thì h ≤ 5 và k ≤ 6

Suy ra diện tích của tam giác S ≤ 18

Vậy diện tích của tam giác có thể bằng 10 \(c{m^2}\)  hay 15 \(c{m^2}\) nhưng không thể bằng 20 \(c{m^2}\)

Câu 30 trang 160 Sách bài tập (SBT) Toán 8 tập 1

Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C.

Giải:                                                          

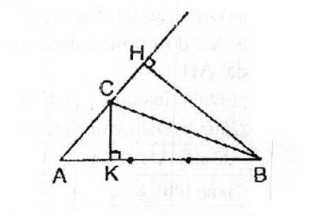
Ta có: \({S_{ABC}} = {1 \over 2}AB.CK = {1 \over 2}AC.BH\)

Suy ra: \(AB.CK = AC.BH\)

\( \Rightarrow {{BH} \over {CK}} = {{AB} \over {AC}}\)

Mà AB = 3 AC (gt) \( \Rightarrow {{BH} \over {CK}} = {{3AC} \over {AC}} = 3\)

Vậy đường cao BH dài gấp 3 lần đường cao CK

Câu 31 trang 160 Sách bài tập (SBT) Toán 8 tập 1

Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành ba đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL (h.187). Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm.

Giải:                                                            

Diện tích hình vuông ABCD bằng \({1 \over 2}\).4.4 = 8 (\(c{m^2}\))

Diện tích tam giác DKN bằng \({1 \over 2}\).4.4 = 8(\(c{m^2}\))

Diện tích phần còn lại là : 36 – ( 8 + 8) = 20 (\(c{m^2}\))

Trong tam giác vuông AEN ta có:

\(E{N^2} = A{N^2} + A{E^2}\)= 4 + 4 = 8

EN = \(2\sqrt 2 \) (cm)

Trong tam giác vuông BHE ta có:

\(E{H^2} = B{E^2} + B{H^2}\)= 16 + 16 = 32

EH = \(4\sqrt 2 \) (cm)

Diện tích hình chữ nhật ENKH bằng  \(2\sqrt 2 \).  \(4\sqrt 2 \) =16 (\(c{m^2}\))

Nối đường chéo BD. Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 \(c{m^2}\)

\({S_{AEPSN}} = {S_{AEN}} + {S_{EPSN}} = 2 + {{16} \over 4} = 6\) ((\(c{m^2}\))

Giaibaitap.me