Câu 12.1 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Hình vuông có chu vi bằng 8 thì đường chéo bằng :
A. 2
B. \(\sqrt {32} \)
C. \(\sqrt 8 \)
D. \(\sqrt 2 \)
Hãy chọn phương án đúng.
Giải:
Chọn C. \(\sqrt 8 \) Đúng
Câu 12.2 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?
Giải:
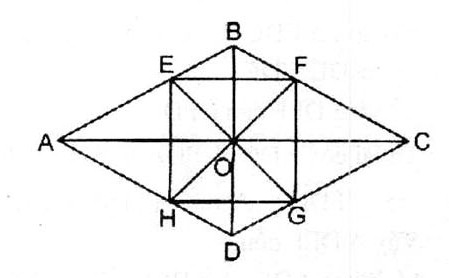
Ta có: \(\widehat {AOB}\)và \)\widehat {COD}\) đối đỉnh nên E, O, G thẳng hàng
\(\widehat {BOC}\)và \(\widehat {AOD}\) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
\(\widehat {EBO} = \widehat {FBO}\) (tính chất hình thoi)
OB cạnh chung
\(\widehat {EOB} = \widehat {FOB} = {45^0}\) (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
\(\widehat {EBO} = \widehat {GDO}\) (so le trong)
OB = OD(tính chất hình thoi)
\(\widehat {EOB} = \widehat {GOD}\) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
\(\widehat {EAO} = \widehat {HAO}\) (tính chất hình thoi)
OA cạnh chung
\(\widehat {EOA} = \widehat {HOA} = {45^0}\) (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.
Câu 12.3 trang 99 Sách bài tập (SBT) Toán 8 tập 1
Cho hình vuông ABCD. Trên cạnh DC lấy điểm E, trên cạnh BC lấy điểm F sao cho DE = CF. Chứng minh rằng AE = DF và AE ⊥ DF.
Giải:
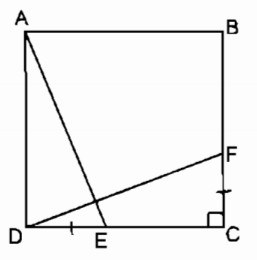
Xét ∆ ADE và ∆ DCF:
AD = DC (gt)
\(\widehat A = \widehat D = {90^0}\)
DE = CF (gt)
Do đó: ∆ ADE = ∆ DCF (c.g.c)
⇒ AE = DF
\(\widehat {EAD} = \widehat {FDC}\)
\((\widehat {EAD} + \widehat {DEA} = {90^0}\) (vì ∆ ADE vuông tại A)
\( \Rightarrow \widehat {FDC} + \widehat {DEA} = {90^0}\)
Gọi I là giao điểm của AE và DF.
Suy ra: \(\widehat {IDE} + \widehat {DEI} = {90^0}\)
Trong ∆ DEI ta có: \(\widehat {DIE} = {180^0} - \left( {\widehat {IDE} + \widehat {DEI}} \right) = {180^0} - {90^0} = {90^0}\)
Suy ra: AE ⊥ DF
Giaibaitap.me
Giải bài tập trang 99, 100 bài ôn tập chương I - tứ giác Sách bài tập (SBT) Toán 8 tập 1. Câu 157: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để EFGH là...
Giải bài tập trang 100, 101 bài ôn tập chương I - tứ giác Sách bài tập (SBT) Toán 8 tập 1. Câu 161: Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC...
Giải bài tập trang 101 bài ôn tập chương I - tứ giác Sách bài tập (SBT) Toán 8 tập 1. Câu I.1: Điền vào chỗ trống...
Giải bài tập trang 155, 156 bài 1 đa giác - đa giác đều Sách bài tập (SBT) Toán 8 tập 1. Câu 1: Trong các hình dưới đây (h.180), hình nào là đa giác lồi ...
