Bài 3.4 trang 132 Sách bài tập (SBT) Hình học 11

Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a. Trên các cạnh bên AA’,BB’,CC’ ta lấy tương ứng các điểm M, N, P sao cho \(AM + BN + CP = a\)

Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.

Giải:

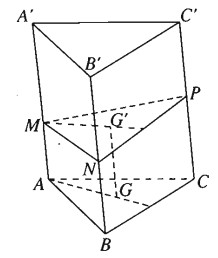
Gọi G và  G’ lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có:

\(\eqalign{
& \,\,\,\,\overrightarrow {GG'} = \overrightarrow {GA} + \overrightarrow {AM} + \overrightarrow {MG'} \cr
& + \,\,\overrightarrow {GG'} = \overrightarrow {GB} + \overrightarrow {BN} + \overrightarrow {NG'} \cr
& \,\,\,\,\,\overrightarrow {GG'} = \overrightarrow {GC} + \overrightarrow {CP} + \overrightarrow {PG'} \cr} \)

Cộng từng vế với vế ta có:

\(3\overrightarrow {GG'}  = \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right) + \left( {\overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP} } \right) + \left( {\overrightarrow {MG'}  + \overrightarrow {NG'}  + \overrightarrow {PG'} } \right)\)

Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \) và G’ là trọng tâm của tam giác MNP nên \(\overrightarrow {MG'}  + \overrightarrow {NG'}  + \overrightarrow {PG'}  = \overrightarrow 0 \).

Do đó: \(3\overrightarrow {GG'}  = \overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP} \)

Hay \(\overrightarrow {GG'}  = {1 \over 3}\left( {\overrightarrow {AM}  + \overrightarrow {BN}  + \overrightarrow {CP} } \right) = {1 \over 3}\overrightarrow {AA'} \)

Vì điểm G cố định và \({1 \over 3}\overrightarrow {AA'} \) là vectơ không đổi nên G’ là điểm cố định. Vậy mặt phẳng  (MNP) luôn luôn đi qua điểm G’ cố định.

Bài 3.5 trang 132 Sách bài tập (SBT) Hình học 11

Trong  không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) đồng phẳng.

Giải:

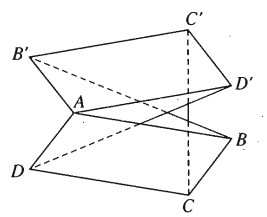
Ta có :

\(\overrightarrow {BB'}  = \overrightarrow {BA}  + \overrightarrow {AB'} ,\overrightarrow {DD'}  = \overrightarrow {DA}  + \overrightarrow {AD'} \) 

Do đó \(\overrightarrow {BB'}  + \overrightarrow {DD'}  = \left( {\overrightarrow {BA}  + \overrightarrow {DA} } \right) + \left( {\overrightarrow {AB'}  + \overrightarrow {AD'} } \right)\)

Vì \(\overrightarrow {BA}  = \overrightarrow {C{\rm{D}}} \) và \(\overrightarrow {AB'}  + \overrightarrow {AD'}  = \overrightarrow {AC'} \)

Nên \(\overrightarrow {BB'}  + \overrightarrow {DD'}  = \left( {\overrightarrow {C{\rm{D}}}  + \overrightarrow {DA} } \right) + \overrightarrow {AC'} \)

Vậy \(\overrightarrow {BB'}  + \overrightarrow {DD'}  = \overrightarrow {CA}  + \overrightarrow {AC'}  = \overrightarrow {CC'} \)

Hệ thức \(\overrightarrow {BB'}  + \overrightarrow {DD'}  = \overrightarrow {CC'} \) biểu thị sự đồng phẳng của ba vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \).

Bài 3.6 trang 132 Sách bài tập (SBT) Hình học 11

Trên mặt phẳng \(\left( \alpha  \right)\) cho hình bình hành \({A_1}{B_1}{C_1}{D_1}\). Về một phía đối với mặt phẳng \(\left( \alpha  \right)\) ta dựng hình bình hành \({A_2}{B_2}{C_2}{D_2}\). Trên các đoạn \({A_1}{A_2},{B_1}{B_2},{C_1}{C_2},{D_1}{D_2}\) ta lần lượt lấy các điểm A, B, C, D sao cho

\({{A{A_1}} \over {A{A_2}}} = {{B{B_1}} \over {B{B_2}}} = {{C{C_1}} \over {C{C_2}}} = {{D{D_1}} \over {D{D_2}}} = 3\) 

Chứng minh rằng tứ giác ABCD là hình bình hành

Giải:

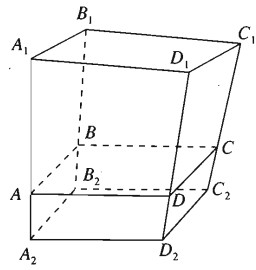
Lấy điểm O cố định rồi đặt \(\overrightarrow {O{A_1}}  = \overrightarrow {{a_1}} ,\,\,\overrightarrow {O{B_1}}  = \overrightarrow {{b_1}} ,\,\,\overrightarrow {O{C_1}}  = \overrightarrow {{c_1}} ,\,\,\overrightarrow {O{D_1}}  = \overrightarrow {{d_1}} \). Điều kiện cần và đủ để tứ giác \({A_1}{B_1}{C_1}{D_1}\) là hình bình hành là \(\overrightarrow {{a_1}}  + \overrightarrow {{c_1}}  = \overrightarrow {{b_1}}  + \overrightarrow {{d_1}} \) ( theo bài tập 3.2)   (1)

Đặt \(\overrightarrow {O{A_2}}  = \overrightarrow {{a_2}} ,\overrightarrow {O{B_2}}  = \overrightarrow {{b_2}} ,\overrightarrow {O{C_2}}  = \overrightarrow {{c_2}} ,\overrightarrow {O{D_2}}  = \overrightarrow {{d_2}} \). Điều kiện cần và đủ để tứ giác \({A_2}{B_2}{C_2}{D_2}\) là hình bình hành là \(\overrightarrow {{a_2}}  + \overrightarrow {{c_2}}  = \overrightarrow {{b_2}}  + \overrightarrow {{d_2}} \)     (2)

Đặt \(\overrightarrow {OA}  = \overrightarrow a ,\,\,\overrightarrow {OB}  = \overrightarrow b ,\,\,\overrightarrow {OC}  = \overrightarrow c ,\,\,\overrightarrow {OD}  = \overrightarrow d \).

Ta có \({{A{A_1}} \over {A{A_2}}} = 3 \Rightarrow \overrightarrow {A{A_1}}  =  - 3\overrightarrow {A{A_2}} \)

\(\eqalign{
& \Leftrightarrow \overrightarrow {O{A_1}} - \overrightarrow {OA} = 3\left( {\overrightarrow {O{A_2}} - \overrightarrow {OA} } \right) \cr
& \Leftrightarrow \overrightarrow {{a_1}} - \overrightarrow a = - 3\left( {\overrightarrow {{a_2}} - \overrightarrow a } \right) \cr
& \Leftrightarrow \overrightarrow a = {1 \over 4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) \cr} \)

Tương tự: \(\overrightarrow b  = {1 \over 4}\left( {\overrightarrow {{b_1}}  + 3\overrightarrow {{b_2}} } \right)\),

\(\overrightarrow c  = {1 \over 4}\left( {\overrightarrow {{c_1}}  + 3\overrightarrow {{c_2}} } \right),\overrightarrow {\,\,d}  = {1 \over 4}\left( {\overrightarrow {{d_1}}  + 3\overrightarrow {{d_2}} } \right)\).

Ta có: \(\overrightarrow a  + \overrightarrow c  = {1 \over 4}\left( {\overrightarrow {{a_1}}  + 3\overrightarrow {{a_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{c_1}}  + 3\overrightarrow {{c_2}} } \right)\)

\(= {1 \over 4}\left( {\overrightarrow {{a_1}}  + \overrightarrow {{c_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{a_2}}  + \overrightarrow {{c_2}} } \right)\)

Và:

\(\eqalign{
& \overrightarrow b + \overrightarrow d = {1 \over 4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right) + {1 \over 4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right) \cr
& = {1 \over 4}\left( {\overrightarrow {{b_1}} + \overrightarrow {{d_1}} } \right) + {3 \over 4}\left( {\overrightarrow {{b_2}} + \overrightarrow {{d_2}} } \right) \cr}\)

Từ (1) và (2) ta có \(\overrightarrow {{a_1}}  + \overrightarrow {{c_1}}  = \overrightarrow {{b_1}}  + \overrightarrow {{d_1}} \) và \(\overrightarrow {{a_2}}  + \overrightarrow {{c_2}}  = \overrightarrow {{b_2}}  + \overrightarrow {{d_2}} \) nên suy ra :

\(\overrightarrow a  + \overrightarrow b  + \overrightarrow c  + \overrightarrow d  \Leftrightarrow \overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OB}  + \overrightarrow {O{\rm{D}}} \)

⟺ tứ giác ABCD là hình bình hành.

Bài 3.7 trang 132 Sách bài tập (SBT) Hình học 11

Cho hình hộp ABCD.A’B’C’D’ có P và R lần lượt là trung điểm các cạnh AB và A’D’. Gọi P’, Q, Q’ lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD’C’, A’B’C’D’, ADD’A’

a) Chứng minh rằng \(\overrightarrow {PP'}  + \overrightarrow {QQ'}  + \overrightarrow {R{\rm{R}}'}  = \overrightarrow 0 \)

b) Chứng minh hai tam giác PQRvà P’Q’R’ có trọng tâm trùng nhau.

Giải:

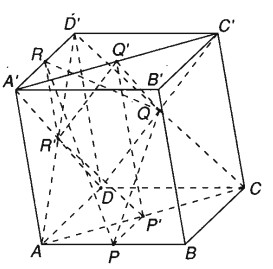
a) Ta có :\(\overrightarrow {PP'}  = {1 \over 2}\overrightarrow {A{\rm{D}}} ,\,\,\,\overrightarrow {QQ'}  = {1 \over 2}\overrightarrow {DA'} ,\,\,\,\overrightarrow {R{\rm{R}}'}  = {1 \over 2}\overrightarrow {A'A} \),

Vậy: \(\overrightarrow {PP'}  + \overrightarrow {QQ'}  + \overrightarrow {R{\rm{R}}'}  = {1 \over 2}\left( {\overrightarrow {A{\rm{D}}}  + \overrightarrow {DA}  + \overrightarrow {A'A} } \right) = \overrightarrow 0 \)

b) Gọi G và G’ lần lượt là trọng tâm các tam giác PQR và P’Q’R’.

Theo câu a) ta có: \(\overrightarrow {PP'}  + \overrightarrow {QQ'}  + \overrightarrow {R{\rm{R}}'}  = \overrightarrow 0 \)

Do đó:

\(\left( {\overrightarrow {PG}  + \overrightarrow {GG'}  + \overrightarrow {G'P'} } \right) + \left( {\overrightarrow {QG}  + \overrightarrow {GG'}  + \overrightarrow {G'Q'} } \right) + \left( {\overrightarrow {RG}  + \overrightarrow {GG'}  + \overrightarrow {G'R'} } \right) = \overrightarrow 0 \)

\( \Leftrightarrow \underbrace {\left( {\overrightarrow {PG}  + \overrightarrow {QG}  + \overrightarrow {RG} } \right)}_{\overrightarrow 0 } + 3\overrightarrow {GG'}  + \underbrace {\left( {\overrightarrow {G'P'}  + \overrightarrow {G'Q'}  + \overrightarrow {G'R'} } \right)}_{\overrightarrow 0 } = \overrightarrow 0 \) 

\(3\overrightarrow {GG'}  = \overrightarrow 0 \) ⟹ G trùng với G’

Vậy hai tam giác PQR và P’Q’R’ có cùng trọng tâm.

Giaibaitap.me