Bài 5 trang 18 sgk giải tích 11
Dựa vào đồ thị hàm số \(y = cosx\), tìm các giá trị của \(x\) để \(cosx = \frac{1}{2}\).
Đáp án :
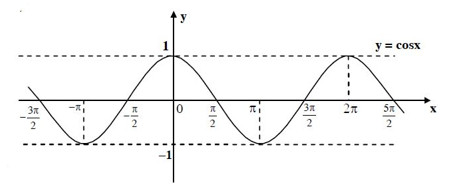
\(cosx = \frac{1}{2}\) là phương trình xác định hoành độ giao điểm của đường thẳng \(y= \frac{1}{2}\) và đồ thị \(y = cosx\).
Từ đồ thị đã biết của hàm số \(y = cosx\) ta xác định giao điểm của nó với đường thẳng \(y= \frac{1}{2}\), ta suy ra \(x = \pm {\pi \over 3} + k2\pi (k \in Z)\), (Các em học sinh nên chú ý tìm giao điểm của đường thẳng cắt đồ thị trong đoạn [-π ; π] và thấy ngay rằng trong đoạn này chỉ có giao điểm ứng với \(x = \pm {\pi \over 3}\) rồi sử dụng tính tuần hoàn để suy ra tất cả các giá trị của \(x\) là \(x = \pm {\pi \over 3} + k2\pi (k \in Z)\).
Bài 6 trang 18 sgk giải tích 11
Dựa vào đồ thị hàm số \(y = sinx\), tìm các khoảng giá trị của \(x\) để hàm số đó nhận giá trị dương.
Đáp án :
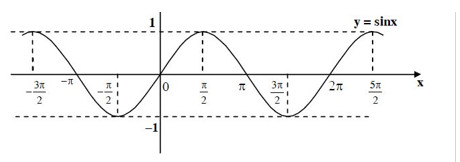
Nhìn đồ thị \(y = sinx\) ta thấy trong đoạn \([-π ; π]\) các điểm nằm phía trên trục hoành của đồ thị \(y = sinx\) là các điểm có hoành độ thuộc khoảng \((0 ; π)\). Từ đó, tất cả các khoảng giá trị của \(x\) để hàm số đó nhận giá trị dương là \((0 + k2π ; π + k2π)\) hay \((k2π ; π + k2π)\) trong đó \(k\) là một số nguyên tùy ý.
Bài 7 trang 18 sgk giải tích 11
Dựa vào đồ thị hàm số \(y = cos x\), tìm các khoảng giá trị của \(x\) để hàm số đó nhận giá trị âm
Trả lời:
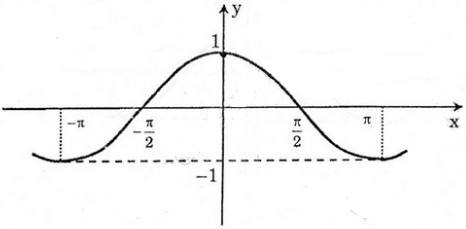
Dựa vào đồ thị hàm số \(y = cosx\), để làm hàm số nhận giá trị âm thì:
\(x \in \left( { - {{3\pi } \over 2}; - {\pi \over 2}} \right);\left( {{\pi \over 2};{{3\pi } \over 2}} \right)... \)
\(\Rightarrow x \in \left( {{\pi \over 2} + k2\pi ;{{3\pi } \over 2} + k2\pi } \right),k \in Z\)
Bài 8 trang 18 sgk giải tích 11
Tìm giá trị lớn nhất của các hàm số:
a) \(y = 2\sqrt{cosx} + 1\) ;
b)\( y = 3 - 2sinx\) .
Đáp án :
a) Với mọi \(x\) thuộc tập xác định của hàm số đã cho ta có
\(0 ≤ cosx ≤ 1\) \(=> y = 2\sqrt{cosx} + 1 ≤ 3\).
Giá trị \(y = 3\) đạt được khi \(cosx = 1 ⇔ x = k2π, k ∈ Z\), do đó \(max \) \(y= 3\).
b) Ta có \(-1 ≤ sinx ≤ 1\), \(∀x\) \(=> 2 ≥ -2sinx ≥ -2\) \(=> 1 ≤ y = 3 – 2sinx ≤ 5,\) \(∀x\) .
Giá trị \(y = 5\) đạt được khi \(sinx = -1\) \(⇔ x \)= \({{ - \pi } \over 2} + k2\pi \), \(k ∈ Z\).
Vậy \(max\) \(y = 5\)
Giaibaitap.me
Giải bài tập trang 28, 29 bài 2 phương trình lượng giác cơ bản Sách giáo khoa (SGK) Giải tích 11. Câu 1: Giải các phương trình sau...
Giải bài tập trang 29 bài 2 phương trình lượng giác cơ bản Sách giáo khoa (SGK) Giải tích 11. Câu 5: Giải các phương trình sau...
Giải bài tập trang 36, 37 bài 3 một số phương trình lượng giác thường gặp Sách giáo khoa (SGK) Giải tích 11. Câu 1: Giải phương trình ...
Giải bài trang 37 bài 3 một số phương trình lượng giác thường gặp Sách giáo khoa (SGK) Giải tích 11. Câu 5: Giải các phương trình sau...
