Bài 2.4 trang 66 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCDcó các điểm M và N lần lượt là trung điểm của ACvà BC. Lấy điểm K thuộc đoạn BD( K không là trung điểm của BD). Tìm giao điểm của đường thẳng AD và mặt phẳng (MNK).
Giải:
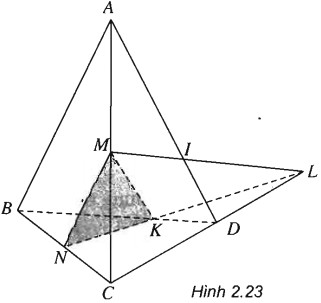
Nhận xét. Trên hình vẽ 2.23 không có sẵn đường thẳng nào của mặt phẳng (MNK) cắt AD. Ta xét mặt phẳng chứa AD chẳng hạn (ACD) rồi tìm giao tuyến ∆ của (ACD) với (MNK). Sau đó tìm giao điểm I của ∆ và AD, I chính là giao điểm phải tìm.
Gọi \(L = NK \cap C{\rm{D}}\)
Ta có \(L \in NK \Rightarrow L \in \left( {MNK} \right)\)
\(L \in C{\rm{D}} \Rightarrow L \in \left( {AC{\rm{D}}} \right)\)
Nên \(ML = \left( {AC{\rm{D}}} \right) \cap \left( {MNK} \right) = \Delta \)
\(\Delta \cap A{\rm{D}} = I \Rightarrow I = \left( {MNK} \right) \cap A{\rm{D}}\)
Bài 2.5 trang 67 Sách bài tập (SBT) Hình học 11
Cho hình chóp S. ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm ( nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp.
Giải:
(h.2.24)
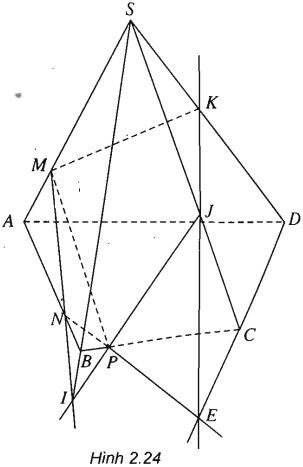
Ta lần lượt tìm giao điểm của mặt phẳng (MNP) với các đường thẳng chứa các cạnh của hình chóp.
Gọi \(I = MN \cap SB\)
Ta có:
\(\left\{ \matrix{
I \in MN \hfill \cr
MN \subset \left( {MNP} \right) \hfill \cr} \right. \Rightarrow I \in \left( {MNP} \right)\)
Vậy \(I = SB \cap \left( {MNP} \right)\).
Từ đó, làm tương tự ta tìm được giao điểm của (MNP) với các cạnh còn lại.
Cụ thể :
Gọi \(J = IP \cap SC\), ta có \(J = SC \cap \left( {MNP} \right)\)
Gọi \(E = NP \cap CD\), ta có \(E = CD \cap \left( {MNP} \right)\)
Gọi \(K = J{\rm{E}} \cap SD\), ta có \(K = SD \cap \left( {MNP} \right)\)
Bài 2.6 trang 67 Sách bài tập (SBT) Hình học 11
Cho hình chóp S.ABCD. M và N tương ứng là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN).
Giải:
(h.2.25)
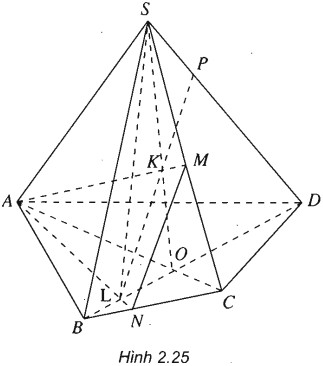
Gọi
\(\eqalign{
& O = AC \cap B{\rm{D}} \cr
& K = SO \cap AN \cr
& L = B{\rm{D}} \cap AN \cr
& P = KL \cap S{\rm{D}} \cr}\)
Ta có \(P = S{\rm{D}} \cap \left( {AMN} \right)\).
Nhận xét . Trong cách giải trên, ta lấy (SBD) là mặt phẳng chứa SD, rồi tìm giao tuyến của (SBD) với (AMN). Từ đó tìm giao điểm của giao tuyến này và SD.
Giaibaitap.me
Giải bài tập trang 67 bài 1 đại cương về đường thẳng và mặt phẳng Sách bài tập (SBT) Hình học 11. Câu 2.7: Cho tứ diện SABC. Trên SA, SB và SC lần lượt lấy các điểm D, E và F sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K...
Giải bài tập trang 70 bài 2 hai đường thẳng chéo nhau và hai đường thẳng song song Sách bài tập (SBT) Hình học 11. Câu 2.10: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Tìm giao tuyến của các cặp mặt phẳng sau đây...
Giải bài tập trang 71 bài hai đường thẳng chéo nhau và hai đường thẳng song song Sách bài tập (SBT) Hình học 11. Câu 2.13: Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD...
Giải bài tập trang 74 bài 3 đường thẳng và mặt phẳng song song Sách bài tập (SBT) Hình học 11. Câu 2.16: Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của tam giác ACD và BCD...
