Bài 2.22 trang 79 Sách bài tập (SBT) Hình học 11

Cho tứ diện ABCD. Gọi  lần lượt là trọng tâm các tam giác . Chứng minh rằng .

Giải:

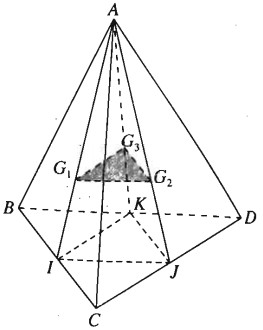
Gọi I, J và K lần lượt là trung điểm của các cạnh BC, CDvà BD. Theo tính chất trọng tâm của tam giác ta có:

\({{A{G_1}} \over {AI}} = {{A{G_2}} \over {AJ}} = {{A{G_3}} \over {AK}} = {2 \over 3}\)

\(\Rightarrow {G_1}{G_2}\parallel IJ\)

\(IJ \subset \left( {BCD} \right) \Rightarrow {G_1}{G_2}\parallel \left( {BCD} \right)\) 

Tương tự ta có \({G_2}{G_3}\parallel \left( {BC{\rm{D}}} \right)\)

\({G_1}{G_2},{G_2}{G_3} \subset \left( {{G_1}{G_2}{G_3}} \right)\)

\(\left( {{G_1}{G_2}{G_3}} \right)\parallel \left( {BC{\rm{D}}} \right)\).

Bài 2.23 trang 79 Sách bài tập (SBT) Hình học 11

Từ bốn đỉnh của hình bình hành ABCD vẽ bốn nửa đường thẳng song song cùng chiều Ax, By, Cz và Dt sao cho chúng cắt mặt phẳng (ABCD). Một mặt phẳng \(\left( \alpha  \right)\) cắt bốn nửa đường thẳng theo thứ tự nói trên tại A’, B’, C’ và D’.

a) Chứng minh rằng \(\left( {Ax,By} \right)\parallel \left( {Cz,Dt} \right)\) và \(\left( {Ax,Dt} \right)\parallel \left( {By,Cz} \right)\)

b) Tứ giác A’B’C’D’ là hình gì?

c) Chứng minh \(AA' + CC' = BB' + DD'\).

Giải:

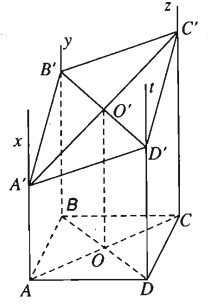
a) Ta có :

\(\left\{ \matrix{
Ax\parallel Dt \hfill \cr
Dt \subset \left( {Cz,Dt} \right) \hfill \cr} \right.\)

\( \Rightarrow Ax\parallel \left( {Cz,Dt} \right)\) 

\(\left. \matrix{
AB\parallel CD \hfill \cr
CD \subset \left( {Cz,Dt} \right) \hfill \cr} \right\} \Rightarrow AB\parallel \left( {Cz,Dt} \right)\)

Từ \(Ax,AB \subset \left( {Ax,By} \right)\) suy ra \(\left( {Ax,By} \right)\parallel \left( {Cz,Dt} \right)\)

Tương tự ta có \(\left( {Ax,Dt} \right)\parallel \left( {By,Cz} \right)\)

b) 

\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {Ax,By} \right) = A'B` \hfill \cr
\left( \alpha \right) \cap \left( {Cz,Dt} \right) = C'D' \Rightarrow A'B'\parallel C'D'\,\,\,\left( 1 \right) \hfill \cr
\left( {Ax,By} \right)\parallel \left( {Cz,Dt} \right) \hfill \cr} \right.\)

\(\left\{ \matrix{
\left( \alpha \right) \cap \left( {Ax,Dt} \right) = A'D` \hfill \cr
\left( \alpha \right) \cap \left( {By,Cz} \right) = B'C' \Rightarrow A'D'\parallel B'C'\,\,\,\left( 2 \right) \hfill \cr
\left( {Ax,Dt} \right)\parallel \left( {By,Cz} \right) \hfill \cr} \right.\)

Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.

c) Gọi O, O’ lần lượt là tâm các hình bình hành ABCD, A’B’C’D’. Dễ thấy OO’ là đường trung bình của hình thang AA’, suy ra \(OO' = {{AA' + CC'} \over 2}\)

Tương tự ta có: 

\(OO' = {{BB' + DD'} \over 2} \Rightarrow AA' + CC' = BB' + DD'\).

Bài 2.24 trang 80 Sách bài tập (SBT) Hình học 11

Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh

a) \(\left( {A{\rm{D}}F} \right)\parallel \left( {BCE} \right)\).

b) \(M'N'\parallel DF\).

c) \(\left( {DEF} \right)\parallel \left( {MM'N'N} \right)\) và \(MN\parallel \left( {DEF} \right)\).

Giải:

a)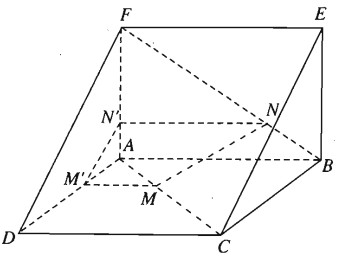

\(\left\{ \matrix{
AD\parallel BC \hfill \cr
BC \subset \left( {BCE} \right) \hfill \cr} \right. \Rightarrow AD\parallel \left( {BCE} \right)\)

\(\left\{ \matrix{
AF\parallel BE \hfill \cr
BE \subset \left( {BCE} \right) \hfill \cr} \right. \Rightarrow AF\parallel \left( {BCE} \right)\)

Mà \(AD,AF \subset \left( {ADF} \right)\)

Nên \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)

b) Vì ABCD và ABEF  là các hình vuông nên AC = BF. Ta có:

\(MM'\parallel C{\rm{D}} \Rightarrow {{AM'} \over {A{\rm{D}}}} = {{AM} \over {AC}}\,\,\,\,\,\,\,\left( 1 \right)\) 

\(NN'\parallel AB \Rightarrow {{AN'} \over {AF}} = {{BN} \over {BF}}\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)

So sánh (1) và (2) ta được \({{AM'} \over {A{\rm{D}}}} = {{AN'} \over {AF}} \Rightarrow M'N'\parallel DF\)

c) Từ chứng minh trên suy ra \(DF\parallel \left( {MM'N'N} \right)\)

\(\left. \matrix{
NN'\parallel AB \Rightarrow NN'\parallel EF \hfill \cr
NN' \subset \left( {MM'N'N} \right) \hfill \cr} \right\} \Rightarrow EF\parallel \left( {MM'N'N} \right)\)

Mà \(DF,EF \subset \left( {DEF} \right)\) nên \(\left( {DEF} \right)\parallel \left( {MM'N'N} \right)\)

Vì \(MN \subset \left( {MM'N'N} \right)\) và \(\left( {MM'N'N} \right)\parallel \left( {DEF} \right)\) nên \(MN\parallel \left( {DEF} \right)\).

Bài 2.25 trang 80 Sách bài tập (SBT) Hình học 11

Cho hình lăng trụ tam giác ABCA’B’C’ có các cạnh bên là AA’, BB’, CC’. Gọi I và I’tương ứng là trung điểm của hai cạnh BC và B’C’.

a) Chứng minh rằng \(AI\parallel A'I'\).

b) Tìm giao điểm của IA’ với mặt phẳng (AB’C’).

c)  Tìm giao tuyến của  (AB’C’) và (A’BC).

Giải:

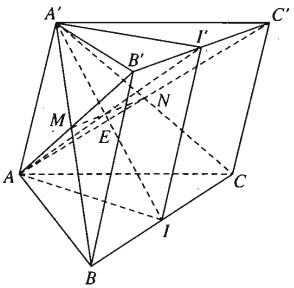
a)  Ta có \(II'\parallel BB'\) và II’ = BB’

Mặt khác \(AA'\parallel BB'\) và AA’ = BB’ nên :

\(AA'\parallel II'\) và AA’ = II’

⇒ AA’II’ là hình bình hành.

\( \Rightarrow AI\parallel A'I'\) 

b) Ta có:

\(\left\{ \matrix{
A \in \left( {AB'C'} \right) \hfill \cr
A \in \left( {AA'I'I} \right) \hfill \cr} \right.\)

\( \Rightarrow A \in \left( {AB'C'} \right) \cap \left( {AA'I'I} \right)\) 

Tương tự : 

\(\left\{ \matrix{
I' \in B'C` \hfill \cr
I' \in \left( {AA'I'I} \right) \hfill \cr} \right. \Rightarrow I' \in \left( {AB'C'} \right)\)

\(I' \in \left( {AB'C'} \right) \cap \left( {AA'I'I} \right) \Rightarrow \left( {AB'C'} \right) \cap \left( {AA'I'I} \right) = AI'\) 

Đặt \(AI' \cap A'I = E\). Ta có:

\(\left\{ \matrix{E \in IA` \hfill \cr E \in AI` \hfill \cr} \right. \Rightarrow E \in \left( {AB'C'} \right)\)

Vậy E là giao điểm của AI’ và mặt phẳng (AB’C’)

c) Ta có:

\(A'B \cap AB' = M \Rightarrow \left\{ \matrix{
M \in \left( {AB'C'} \right) \hfill \cr
M \in \left( {A'BC} \right) \hfill \cr} \right.\)

Tương tự:

\(AC' \cap A'C = N \Rightarrow \left\{ \matrix{
N \in \left( {AB'C'} \right) \hfill \cr
N \in \left( {A'BC} \right) \hfill \cr} \right.\)

Vậy \(\left( {AB'C'} \right) \cap \left( {A'BC} \right) = MN\).

Giaibaitap.me