Bài 2.26 trang 80 Sách bài tập (SBT) Hình học 11

Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của A’B’.

a) Chứng minh rằng \(CB'\parallel \left( {AHC'} \right)\)

b) Tìm giao tuyến d của (AB’C’) và (ABC)

Giải:

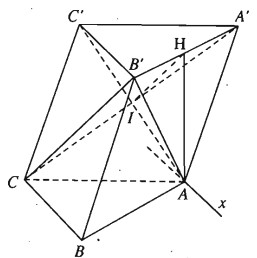
a)  Ta có tứ giác AA’CC’  là hình bình hành suy ra A’C cắt AC’ tại trung điểm I của mỗi đường.

Do đó \(IH\parallel CB'\) ( đường trung bình của tam giác CB’A’)

Mặt khác \(IH \subset \left( {AHC'} \right)\) nên \(CB'\parallel \left( {AHC'} \right)\)

b) Ta có:

\(\left\{ \matrix{
A \in \left( {AB'C'} \right) \hfill \cr
A \in \left( {ABC} \right) \hfill \cr} \right.\)

⇒ A là điểm chung của (AB’C’) và (ABC)

Mà

\(\left\{ \matrix{
B'C'\parallel BC \hfill \cr
B'C' \subset \left( {AB'C'} \right) \hfill \cr
BC \subset \left( {ABC} \right) \hfill \cr} \right.\)

Nên \(\left( {AB'C'} \right) \cap \left( {ABC} \right) = Ax\)

Và \(Ax\parallel BC\parallel B'C'\)

Bài 2.27 trang 80 Sách bài tập (SBT) Hình học 11

Cho hai hình bình hành ABCD và ABEF không nằm cùng trong một mặt phẳng. Gọi M và N là hai điểm di động tương ứng trên  AD và BE sao cho

\({{AM} \over {M{\rm{D}}}} = {{BN} \over {NE}}\) 

Chứng minh rằng đường thẳng MN luôn luôn song song với một mặt phẳng cố định. Hãy chỉ ra mặt phẳng cố định đó.

Giải:

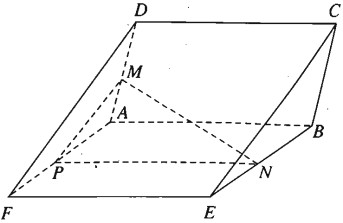
Trong mặt phẳng (ADF), kẻ đường thẳng \(MP\parallel DF\left( {P \in AF} \right)\)

Ta có \({{AP} \over {PF}} = {{AM} \over {M{\rm{D}}}} = {{BN} \over {NE}}\)

Nên \(PN\parallel F{\rm{E}}\). Do đó \(\left( {MNP} \right)\parallel \left( {DEF} \right)\).

Vậy MN song song với mặt phẳng (DEF) cố định.

Bài 2.28 trang 80 Sách bài tập (SBT) Hình học 11

Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với . Lấy là mặt phẳng đi qua I và song song với mặt phẳng (SBD).

a) Xác định thiết diện của mặt phẳng  với hình chóp S.ABCD.

b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.

Giải:

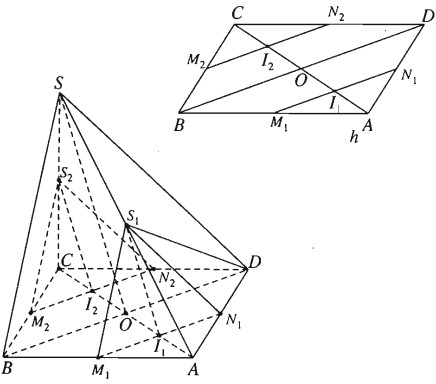
a) Trường hợp 1 .

I  thuộc đoạn \(AO\left( {0 < x < {a \over 2}} \right)\)

Khi đó I ở vị trí I₁

Ta có: \(\left( \alpha  \right)\parallel \left( {SB{\rm{D}}} \right)\)

\( \Rightarrow \left\{ \matrix{
\left( \alpha \right)\parallel B{\rm{D}} \hfill \cr
\left( \alpha \right)\parallel SO \hfill \cr} \right.\) 

Vì \(\left( \alpha  \right)\parallel BD\) nên \(\left( \alpha  \right)\) cắt (ABD) theo giao tuyến  M₁N₁ ( qua I₁) song song với BD

Tương tự \(\left( \alpha  \right)\parallel SO\) nên \(\left( \alpha  \right)\) cắt (SOA) theo giao tuyến

S₁I₁ song song với SO.

Ta có thiết diện trong trường hợp này là tam giác \({S_1}{M_1}{N_1}\).

Nhận xét. Dễ thấy rằng \({S_1}{M_1}\parallel SB\) và \({S_1}{N_1}\parallel S{\rm{D}}\). Lúc đó tam giác \({S_1}{M_1}{N_1}\) đều.

Trường hợp 2. I thuộc đoạn \(OC\left( {{a \over 2} < x < a} \right)\)

Khi đó I ở vị trí I₂. Tương tự như trường hợp 1 ta có thiết diện là tam giác đều \({S_2}{M_2}{N_2}\) có \({M_2}{N_2}\parallel B{\rm{D}}\), \({S_2}{M_2}\parallel SB\), \({S_2}{N_2}\parallel S{\rm{D}}\).

Trường hợp 3. \(I \equiv O\). Thiết diện chính là tam giác đều SBD.

b) Ta lần lượt tìm diện tích thiết diện trong các trường hợp 1,2,3.

Trường hợp 1 . I  thuộc đoạn \(AO\left( {0 < x < {a \over 2}} \right)\)

\({{{S_{{S_1}{M_1}{N_1}}}} \over {{s_{SB{\rm{D}}}}}} = {\left( {{{{M_1}{N_1}} \over {B{\rm{D}}}}} \right)^2} = {\left( {{{2x} \over a}} \right)^2}\)

\({S_{{S_1}{M_1}{N_1}}} = {{4{{\rm{x}}^2}} \over {{a^2}}}.{S_{SB{\rm{D}}}} = {{4{{\rm{x}}^2}} \over {{a^2}}}.{{{b^2}\sqrt 3 } \over 4} = {{{b^2}{x^2}\sqrt 3 } \over {{a^2}}}\) 

Trường hợp 2 . I thuộc đoạn \(OC\left( {{a \over 2} < x < a} \right)\)

\({{{S_{{S_2}{M_2}{N_2}}}} \over {{S_{SBD}}}} = {\left( {{{{M_2}{N_2}} \over {BD}}} \right)^2} = \left[ {{{2{{\left( {a - x} \right)}^2}} \over a}} \right]\) 

\({S_{{S_2}{M_2}{N_2}}} = {4 \over {{a^2}}}{\left( {a - x} \right)^2}.{{{b^2}\sqrt 3 } \over 4} = {{{b^2}\sqrt 3 } \over {{a^2}}}{\left( {a - x} \right)^2}\)

Trường hợp 3. \(I \equiv O\)  .

\({S_{SBD}} = {{{b^2}\sqrt 3 } \over 4}\)

Tóm lại

\({S_{thiết\,diện}} = \left\{ \matrix{
{{{b^2}{x^2}\sqrt 3 } \over {{a^2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,nếu\,\,0 < x < {a \over 2} \hfill \cr
{{{b^2}\sqrt 3 } \over 4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,nếu\,\,x = {a \over 2} \hfill \cr
{{{b^2}\sqrt 3 } \over {{a^2}}}{\left( {a - x} \right)^2}\,\,nếu\,\,{a \over 2} < x < a\, \hfill \cr} \right.\)

* Đồ thị của hàm số S theo biến x như sau: 

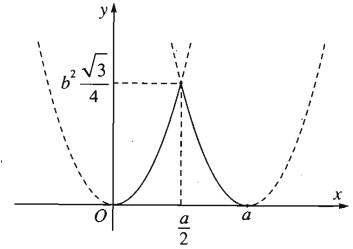
Vậy S_{thiết diện} lớn nhất  khi và chỉ khi \(x = {a \over 2}\).

Bài 2.29 trang 80 Sách bài tập (SBT) Hình học 11

Cho ba mặt phẳng \(\left( \alpha  \right),\left( \beta  \right),\left( \gamma  \right)\) song song với nhau. Hai đường thẳng a và a’ cắt ba mặt phẳng ấy theo thứ tự nói trên tại A, B, C vàA’, B’, C’. Cho \(AB = 5,BC = 4,A'C' = 18\). Tính độ dài.A’B’, B’C’

Giải:

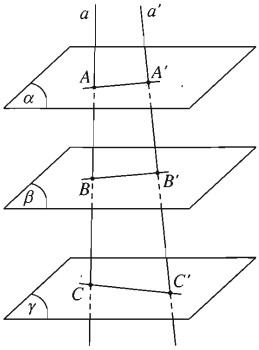
Vì \(\left( \alpha  \right)\parallel \left( \beta  \right)\parallel \left( \gamma  \right)\) nên \({{AB} \over {A'B'}} = {{BC} \over {B'C'}}\)

Mặt khác ta có:

\({{AB} \over {A'B'}} = {{BC} \over {B'C'}} = {{AB + BC} \over {A'B' + B'C'}} = {{AC} \over {A'C'}}\) 

Suy ra: \(A'B' = {{A'C'.AB} \over {AC}} = {{18.5} \over 9} = 10\)

Vậy  A’B’ = 10 và \(B'C' = {{A'C'.BC} \over {AC}} = {{18.4} \over 9} = 8\)

Vậy B’C’ = 8.

Giaibaitap.me