Bài 2.35 trang 83 Sách bài tập (SBT) Hình học 11
Hãy vẽ hình biểu diễn của một đường tròn cùng với hai đường kính vuông góc của đường tròn đó.
Giải:
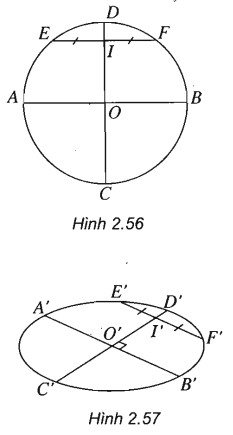
(h.2.56) Giả sử trên hình thực ta có đường tròn tâm O cùng với hai đường kính vuông góc của đường tròn đó là AB và CD. Nếu ta vẽ thêm một dây cung EF song song với AB thì đường kính CD sẽ đi qua trung điểm I của đoạn EF. Từ đó ta suy ra cách vẽ sau đây:
a) (h.2.57) Vẽ hình elip biểu diễn cho đường tròn và vẽ đường kính A’B’ của hình elip đó. Đường kính này đi qua tâm O’ của elip.
b) Vẽ một dây cung E’F’ song song với đường kính A’B’. Gọi I’ là trung điểm của E’F’. Đường thẳng O’I’cắt elip tại hai điểm C’ và D’. Ta có A’B’ và C’D’ là hình biểu diễn của hai đường kính vuông góc với nhau của đường tròn.
Nhận xét. Hình bình hành A’C’B’D’là hình biểu diễn của hình vuông ACBD nội tiếp trong một đường tròn.
Bài 2.36 trang 83 Sách bài tập (SBT) Hình học 11
Hãy chọn phép chiếu song song với phương chiếu của và mặt phẳng chiếu thích hợp để hình chiếu song song của một tứ diện cho trước là một hình bình hành.
Giải:
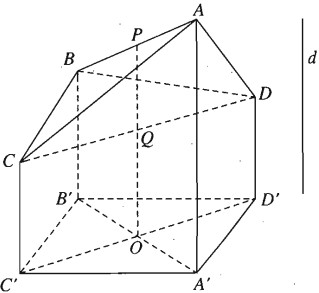
Cho tứ diện ABCD. Gọi d là một đường thẳng không song song với với các cạnh của tứ diện và \(\left( \alpha \right)\) là một mặt phảng cắt d. Gọi A’, B’, C’, D’ lần lượt là hình chiếu của A, B, C, D trên mặt phẳng \(\left( \alpha \right)\). Gọi P và Q lần lượt là trung điểm của hai cạnh đối diện AB và CD. Khi đó hình chiếu của P’ và Q’ của P và Q sẽ lần lượt là trung điểm của
A’B’ và C’D’.
Muốn cho A’, B’, C’, D’ là các đỉnh của một hình bình hành ta chỉ cần chọn phương chiếu d sao cho d song song với đường thẳng PQ.
Vậy để hình chiếu song song của một tứ diện là một hình bình hành ta có thể chọn :
- Phương chiếu d là phương của một trong ba đường thẳng đi qua trung điểm của hai cạnh đối diện của tứ diện cho trước.
- Mặt phẳng chiếu \(\left( \alpha \right)\) là mặt phẳng tùy ý, nhưng phải cắt đường thẳng d.
Giaibaitap.me
Giải bài tập trang 84 bài ôn tập chương II đường thẳng và mặt phẳng trong không gian. Quan hệ song song Sách bài tập (SBT) Hình học 11. Câu 2.37: Chứng minh rằng ...
Giải bài tập trang 84 bài ôn tập chương II đường thẳng và mặt phẳng trong không gian. Quan hệ song song Sách bài tập (SBT) Hình học 11. Câu 2.41: Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)...
Giải bài tập trang 86 bài đề toán tổng hợp Sách bài tập (SBT) Hình học 11. Câu 2.49: Cho tứ diện ABCD. Trên ba cạnh AB, AC, AD lần lượt lấy các điểm B’, C’, D’ sao cho ...
Giải bài tập trang 87 bài đề toán tổng hợp Sách bài tập (SBT) Hình học 11. Câu 2.52: Cho hình chóp S.ABCD. Gọi E, F, G lần lượt là các điểm thuộc miền trong các tam giác SAB, SBC, SCD...
