Bài 1.5 trang 13 Sách bài tập (SBT) Đại số và giải tích 11
Xác định tính chẵn lẻ của các hàm số
a) \(y = {{\cos 2x} \over x}\)
b) \(y = x - \sin x\)
c) \(y = \sqrt {1 - \cos x} \)
d) \(y = 1 + \cos x\sin \left( {{{3\pi } \over 2} - 2x} \right)\)
Giải
a) \(y = {{\cos 2x} \over x}\) là hàm số lẻ
b) \(y = x - \sin x\) là hàm số lẻ
c) \(y = \sqrt {1 - \cos x} \) là hàm số chẵn
d) \(y = 1 + \cos x\sin \left( {{{3\pi } \over 2} - 2x} \right)\) là hàm số chắn
Bài 1.6 trang 13 Sách bài tập (SBT) Đại số và giải tích 11
a) Chứng minh rằng \(\cos 2\left( {x + k\pi } \right) = \cos 2x,k \in Z\) . Từ đó vẽ đồ thị hàm số y = cos 2x
b) Từ đồ thị hàm số y = cos 2x, hãy vẽ đồ thị hàm số y = |cos 2x|
Giải:
a) \(\cos 2(x + k\pi ) = \cos (2x + k2\pi ) = \cos 2x,k \in Z\). Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos 2x
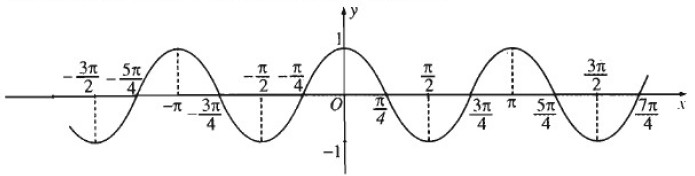
b) Đồ thị hàm số y = |cos 2x|
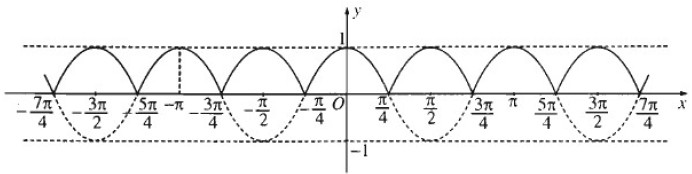
Bài 1.7 trang 13 Sách bài tập (SBT) Đại số và giải tích 11
Hãy vẽ đồ thị của các hàm số
a) y = 1 + sin x
b) y = cos x - 1
c) \(y = \sin \left( {x - {\pi \over 3}} \right)\)
d) \(y = \cos \left( {x + {\pi \over 6}} \right)\)
Giải:
a) Đồ thị hàm số y = 1 + sin x thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục tung lên phía trên một đơn vị.
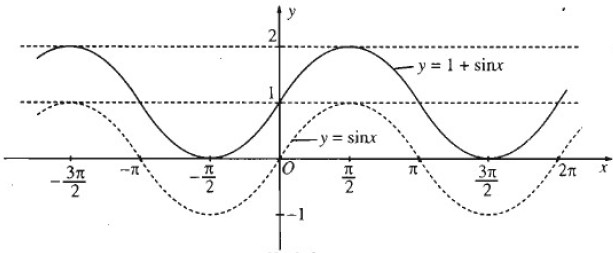
b) Đồ thị hàm số y = cos x - 1 thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục tung xuống phía dưới một đơn vị.
c) Đồ thị hàm số \(y = \sin \left( {x - {\pi \over 3}} \right)\) thu được từ đồ thị hàm số y = sinx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \({\pi \over 3}\)
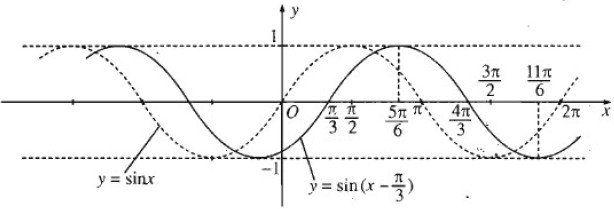
d) Đồ thị hàm số \(y = \cos \left( {x + {\pi \over 6}} \right)\) thu được từ đồ thị hàm số y = cosx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng \({\pi \over 6}\)
Bài 1.8 trang 13 Sách bài tập (SBT) Đại số và giải tích 11
Hãy vẽ đồ thị của các hàm số
a) \(y = \tan \left( {x + {\pi \over 4}} \right)\)
b) \(y = \cot \left( {x - {\pi \over 6}} \right)\)
Giải:
a) Đồ thị hàm số \(y = \tan \left( {x + {\pi \over 4}} \right)\) thu được từ đồ thị hàm số y = tanx bằng cách tịnh tiến song song với trục hoành sang trái một đoạn bằng \({\pi \over 4}\).
b) Đồ thị hàm số \(y = \cot \left( {x - {\pi \over 6}} \right)\) thu được từ đồ thị hàm số y = cotx bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \({\pi \over 6}\)
Giaibaitap.me
Giải bài tập trang 22 bài 2 phương trình lượng giác cơ bản Sách bài tập (SBT) Đại số và giải tích 11. Câu 2.1: Giải các phương trình...
Giải bài tập trang 23 bài 2 phương trình lượng giác cơ bản Sách bài tập (SBT) Đại số và giải tích 11. Câu 2.4: Giải các phương trình...
Giải bài tập trang 35, 36 bài một số phương trình lượng giác cơ bản Sách bài tập (SBT) Đại số và giải tích 11. Câu 3.1: Giải các phương trình sau...
Giải bài tập trang 36 bài 3 một số phương trình lượng giác cơ bản Sách bài tập (SBT) Đại số và giải tích 11. Câu 3.5:
