Câu 58 trang 98 Sách bài tập (SBT) Toán 8 tập 2

Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E,F thuộc phần kéo dài của các cạnh AB và AD). Chứng minh rằng AB.AE + AD.AF = \(A{C^2}\).

Giải:

(hình trang 123 sgbt)

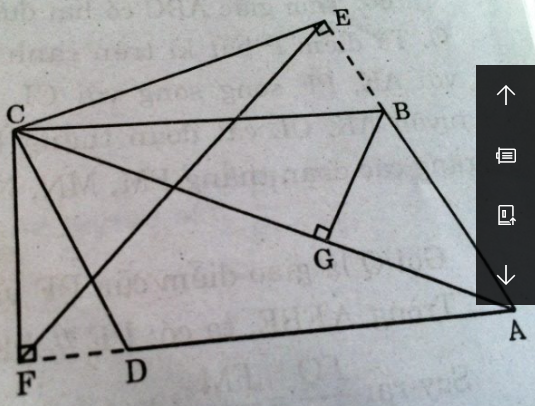
Dựng BG ⊥ AC.

Xét ∆ BGA và ∆ CEA, ta có:

\(\widehat {BGA} = \widehat {CEA} = 90^\circ \)

\(\widehat A\) chung

Suy ra: ∆ BGA đồng dạng ∆ CEA (g.g)

Suy ra: \({{AB} \over {AC}} = {{AG} \over {AE}}\)

Suy ra: AB.AE = AC.AG   (1)

Xét ∆ BGC và ∆ CFA, ta có:

\(\widehat {BGC} = \widehat {CFA} = 90^\circ \)

\(\widehat {BCG} = \widehat {CAF}\)  (so le trong vì AD // BC)

Suy ra: ∆ BGC đồng dạng ∆ CFA (g.g)

Suy ra: \({{AF} \over {CG}} = {{AC} \over {BC}} \Rightarrow BC.AF = AC.CG\)

Mà BC = AD (tính chất hình bình hành )

Suy ra: AD.AF = AC.CG            (2)

Cộng từng vế của đẳng thức (1) và (2) ta có:

AB.AE + AD.AF = AC.AG + AC.CG

\( \Rightarrow AB.AE + AD.AF = AC\left( {AG + CG} \right)\)

Mà \(AG + CG = AC\)  nên \(AB.AE + AD.AF = A{C^2}\)

Câu 59 trang 98 Sách bài tập (SBT) Toán 8 tập 2

Tam giác ABC có hai đường cao là AD và BE (D thuộc BC, E thuộc AC).

Chứng minh hai tam giác DEC  và ABC là hai tam giác đồng dạng.

Giải:

(hình trang 124 sgbt)

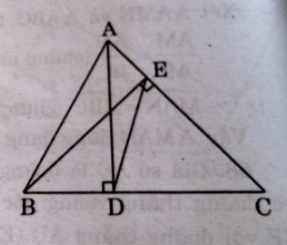
Xét ∆ ADC và ∆ BEC, ta có:

\(\widehat {ADC} = \widehat {BEC} = 90^\circ \)

\(\widehat C\)  chung

Suy ra: ∆ ADC đồng dạng ∆ BEC (g.g)

Suy ra: \({{AC} \over {BC}} = {{DC} \over {EC}} \Rightarrow {{EC} \over {BC}} = {{DC} \over {AC}}\)

Xét ∆ DEC và ∆ ABC, ta có:

\({{EC} \over {BC}} = {{DC} \over {AC}}\)

\(\widehat C\) chung

Vậy ∆ DEC đồng dạng ∆ ABC (c.g.c)

Câu 60 trang 98 Sách bài tập (SBT) Toán 8 tập 2

Tam giác ABC có hai trung tuyến AK và CL cắt nhau tại O. Từ một điểm P bất kì trên cạnh AC, vẽ các đường thẳng PE song song với AK, PF song song với CL (E thuộc BC, F thuộc AB). Các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự tại M, N

Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau.

 Giải:

(hình trang 125 sgbt)

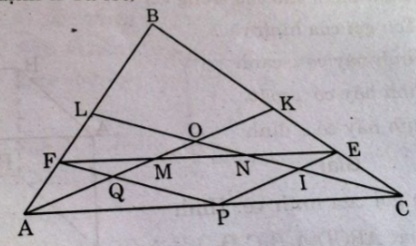
Gọi Q là giao điểm của PF và AK, I là giao điểm của PE và CL.

Trong tam giác FBE, ta có:

PE // AK hay QM // PE

Suy ra: \({{FQ} \over {FB}} = {{FM} \over {FE}}\) (Định lí Ta-lét )         (1)

Trong tam giác ALO, ta có:

PF // CL hay FQ // LO

Suy ra: \({{AF} \over {AL}} = {{FQ} \over {LO}}\)  (Định lí Ta-lét )                      (2)

Trong tam giác ALC,ta có:

PF // CL

Suy ra: \({{AF} \over {AL}} = {{FP} \over {CL}}\)  (Định lí Ta-lét )                         (3)

Từ (2) và (3) suy ra \({{FQ} \over {LO}} = {{FP} \over {CL}} \Rightarrow {{FQ} \over {FP}} = {{LO} \over {CL}}\)

Vì LO = \({1 \over 3}\) CL (tính chất đường trung tuyến) nên \({{FQ} \over {FP}} = {1 \over 3}\)                  (4)

Từ (1) và (4) suy ra \({{FM} \over {FE}} = {1 \over 3} \Rightarrow FM = {1 \over 3}FE\)

Trong tam giác EBF, ta có:

 PF // CL hay NI // PF

Suy ra: \({{EI} \over {EP}} = {{EN} \over {EF}}\)  (Định lí Ta-lét )                               (5)

Trong tam giác CKO, ta có: EI // OK

Suy ra: \({{CE} \over {CK}} = {{EI} \over {KO}}\)  (Định lí Ta-lét )         (6)

Trong tam giác CKA, ta có: PE // AK

Suy ra: \({{CE} \over {CK}} = {{EP} \over {AK}}\)  (Định lí Ta-lét )         (7)

Từ (6) và (7) suy ra :

 \(\eqalign{  & {{EI} \over {OK}} = {{EP} \over {AK}}  \cr  &  \Rightarrow {{EI} \over {EP}} = {{OK} \over {AK}} \cr} \)

Vì OK = \({1 \over 3}\)AK (tính chất đường trung tuyến) nên:

\({{EI} \over {EP}} = {1 \over 3}\)                   (8)

Từ (5) và (8) suy ra :

\(\eqalign{  & {{EN} \over {EF}} = {1 \over 3}  \cr  &  \Rightarrow EN = {1 \over 3}EF \cr} \)

Ta có:

\(\eqalign{  & MN = EF - \left( {EN + FM} \right)  \cr  &  = EF - \left( {{1 \over 3}EF + {1 \over 3}EF} \right) = {1 \over 3}EF \cr} \)

Vậy EN = MN = NF.

 Giaibaitap.me