Bài 1.31 trang 39 Sách bài tập (SBT) Hình học 11

Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(3x - 5y + 3 = 0\) và vectơ \(\overrightarrow v  = \left( {2;3} \right)\). Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ \(\overrightarrow v \).

Giải:

Gọi \(M'(x';y') \in d'\) là ảnh của \(M(x,y) \in d\) qua phép tịnh tiến theo vecto \(\vec v(2;3)\)

\( \Rightarrow \left\{ \matrix{
x' = x + 2 \hfill \cr
y' = y + 3 \hfill \cr} \right. \Rightarrow \left\{ \matrix{
x = x' - 2 \hfill \cr
y = y' - 3 \hfill \cr} \right.\)

Do \(M(x,y) \in d\) nên

\(\eqalign{
& 3x - 5y + 3 = 0 \cr
& \Rightarrow 3(x' - 2) - 5(y' - 3) + 3 = 0 \cr
& \Leftrightarrow 3x' - 5y' + 12 = 0{\rm{ }}(d') \cr} \)

Vậy \(M'(x';y') \in d':3x' - 5y' + 12 = 0\)

Bài 1.32 trang 39 Sách bài tập (SBT) Hình học 11

Cho hình bình hành ABCD có ABcố định, đường chéo ACcó độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.

Giải:

Xem D là ảnh của C qua phép tịnh tiến theo vectơ \(\overrightarrow {BA} \). Do C chạy trên đường tròn (C) tâm A bán kính m, trừ ra giao điểm của (C) với đường thẳng AB, nên D thuộc đường tròn là ảnh của đường tròn nói trên qua phép tịnh tiến theo vectơ \(\overrightarrow {BA} \).

Bài 1.33 trang 39 Sách bài tập (SBT) Hình học 11

Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Giải:

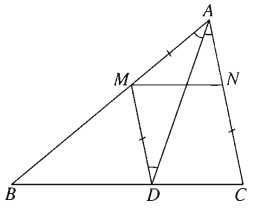
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó \(\widehat {MA{\rm{D}}} = \widehat {M{\rm{D}}A} = \widehat {DAC}\). Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có \(\overrightarrow {NM}  = \overrightarrow {C{\rm{D}}} \), nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ \(\overrightarrow {DC} \).

Từ đó suy ra cách dựng:

-  Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.

- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ \(\overrightarrow {C{\rm{D}}} \). d cắt AB tại M.

-  Dựng N sao cho \(\overrightarrow {NM}  = \overrightarrow {C{\rm{D}}} \).

Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.

Bài 1.34 trang 39 Sách bài tập (SBT) Hình học 11

Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(3x - 2y - 6 = 0\)  

a)  Viết phương trình của đường thẳng \(d_1\) là ảnh của d qua phép đối xứng qua trục Oy

b)  Viết phương trình của đường thẳng \(d_2\) là ảnh của d qua phép đối xứng qua đường thẳng ∆ có phương trình \(x + y - 2 = 0\).

Giải:

a) \({d_1}:3{\rm{x}} + 2y + 6 = 0\)

b) Giao của d và ∆ là \(A\left( {2;0} \right)\). Lấy \(B\left( {0; - 3} \right)\) thuộc d. Ảnh của B qua phép  đối xứng của đường thẳng ∆ là \(B'\left( {5;2} \right)\). Khi đó d' chính là đường thẳng \(AB':2{\rm{x}} - 3y - 4 = 0\)

Giaibaitap.me