Bài 1 trang 46 sgk đại số và giải tích 11.

Từ các chữ số \(1, 2, 3, 4\) có thể lập được bao nhiêu số tự nhiên gồm:

a) Một chữ số ?        b) Hai chữ số ?    

c) Hai chữ số khác nhau ?

Bài giải:

a) \(4\) số.

b) Số tự nhiên cần lập có dạng \(\overline{ab}\), với \(a, b ∈ \left\{{1, 2, 3, 4}\right\}\) có kể đến thứ tự.

Để lập được số tự nhiên này, phải thực hiện liên tiếp hai hành động sau đây:

Hành động 1: Chọn chữ số \(a\) ở hàng chục. Có \(4\) cách để thực hiện hành động này

Hành động 2: Chọn chữ số \(b\) ở hàng đơn vị. Có \(4\) cách để thực hiện hành động này.

Theo quy tắc nhân suy ra số các cách để lập được số tự nhiên kể trên là

                     \(4 . 4 = 16\) (cách).

Qua trên suy ra từ các chữ số đã cho có thể lập được \(16\) số tự nhiên có hai chữ số.

c) Số tự nhiên cần lập có dạng \(\overline{ab}\), với \(a, b ∈ \left\{{1, 2, 3, 4}\right\}\) và \(a, b\) phải khác nhau, có kể đến thứ tự.

Để lập được số tự nhiên này, phải thực hiện liên tiếp hai hành động sau đây:

Hành động 1: Chọn chữ số \(a\) ở hàng chục.

Có \(4\) cách để thực hiện hành động này.

Hành động 2: Chọn chữ số b ở hàng đơn vị, với \(b\) khác chữ số \(a\) đã chọn.

Có \(3\) cách để thực hiện hành động này.

Theo quy tắc nhân suy ra từ các cách để lập được số tự nhiên kể trên là:

               \(4 . 3 = 12\) (cách).

Qua trên suy ra từ các chữ số đã cho có thể lập được \(12\) số tự nhiên có hai chữ số khác nhau.

Bài 2 trang 46 sgk đại số và giải tích 11.

Từ các chữ số \(1, 2, 3, 4, 5, 6\) có thể lập được bao nhiêu số tự nhiên bé hơn \(100\) ?

Bài giải:

Mỗi số tự nhiên cần lập là số tự nhiên có không quá \(2\) chữ số, được lập từ các chữ số \(1, 2, 3, 4, 5, 6\).

Để lập được số tự nhiên như vậy, phải thực hiện một hành động trong hai hành động loại trừ nhau sau đây:

Hành động 1: Từ các chữ số \(1, 2, 3, 4, 5, 6\) lập số tự nhiên có một chữ số.

Có \(6\) cách để thực hiện hành động này.

Hành động 2: Từ các chữ số \(1, 2, 3, 4, 5, 6\) lập số tự nhiên có hai chữ số.

Vận dụng quy tắc nhân, ta tìm được: Có \(6^2 = 36\) cách để thực hiện hành động này.

Theo quy tắc cộng suy ra số các cách để lập được các số tự nhiên kể trên là

                              \(6 + 36 = 42\) (cách).

Qua trên suy ra từ các chữ số đã cho có thể lập được \(42\) số tự nhiên bé hơn \(100\).

Bài 3 trang 46 sgk đại số và giải tích 11.

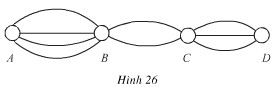
Các thành phố \(A, B, C, D\) được nối với nhau bởi các con đường như hình 26. Hỏi:

a) Có bao nhiêu cách đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần ?

b) Có bao nhiêu cách đi từ \(A\) đến \(D\) rồi quay lại \(A\) ?

Bài giải:

a) Để đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:

Hành động 1: Đi từ \(A\) đến \(B\). Có \(4\) cách để thực hiện hành động này.

Hành động 2: Đi từ \(B\) đến \(C\). Có \(2\) cách để thực hiện hành động này.

Hành động 3: Đi từ \(C\) đến \(D\). Có \(3\) cách để thực hiện hành động này.

Theo quy tắc nhân suy ra số các cách để đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần là \(4 . 2 . 3 = 24\) (cách).

b) ĐS: Số các cách để đi từ \(A\) đến \(D\) (mà qua \(B\) và \(C\) chỉ một lần), rồi quay lại \(A\) (mà qua \(C\) và \(B\) chỉ một lần) là:

               \((4 . 2 . 3) . (3 . 2 . 4) = 24^2 = 576\) (cách).

Bài 4 trang 46 sgk đại số và giải tích 11.

Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da,, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây ?

Bài giải:

Có ba kiểu mặt đồng hồ nên có ba cách chọn mặt.

Có bốn kiểu dây nên có bốn cách chọn dây.

Vậy có \(3 . 4 = 12\) cách để chọn một chiếc đồng hồ.

Giaibaitap.me