Bài 1 trang 77 sách giáo khoa hình học lớp 11
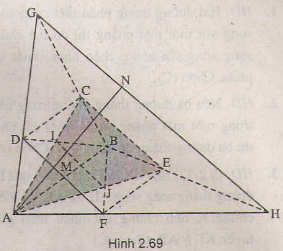
Cho hai hình thang \(ABCD\) và \(ABEF\) có chung đáy lớn \(AB\) và không cùng nằm trong một mặt phẳng.
a) Tìm giao tuyến của các mặt phắng sau: \((AEC)\) và \((BFD)\), \((BCE)\) và \((ADF)\)
b) Lấy \(M\) là điểm thuộc \(DF\). Tìm giao điểm của đường thẳng \(AM\) với mặt phẳng \((BCE)\)
c) Chứng minh hai đường thẳng \(AC\) và \(BF\) không cắt nhau
Lời giải:
a) Trong \((ABCD)\) : Gọi \(I=AC ∩ BD \), Trong \(( ABEF)\): Gọi \(J=AE ∩ BF \)
\(\Rightarrow (ACE) ∩ (BDF) = IJ\).
Tương tự \((BCE) ∩ ( ADF) = GH\)
b) Trong \((AGH)\): Gọi \(N=AM ∩ GH\), \(N \in AM\) và \(N \in GH\subset (BCE)\)
Do đó: \(N=AM\cap(BCE)\)
c) Chứng minh bằng phương pháp phản chứng.
Giả sử \(AC\) và \(BE\) cùng nằm trong một mặt phẳng, lập luận dẫn tới \((ABCD) ≡ (ABEF)\) hay chúng cùng nằm trong một mặt phẳng (trái với giả thiết)
Do đó: \(AC\) và \(BF\) không cắt nhau.
Bài 2 trang 77 sách giáo khoa hình học lớp 11
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M, N, P\) theo thứ tự là trung điểm của các đoạn thẳng \(SA, BC, CD\). Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng \((MNP)\)
Gọi \(O\) là giao diểm hai đường chéo của hình bình hành \(ABCD\), hãy tìm giao điểm của đường thẳng \(SO\) với \(mp (MNP)\).
Lời giải:
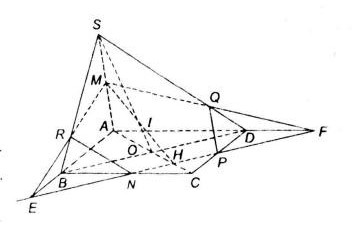
a) Trong mặt phẳng \((ABCD)\) đường thẳng \(NP\) cắt đường thẳng \(AB, AD\) lần lượt tại \(E, F\).
Trong mặt phẳng\((SAD)\) gọi \(Q=SD\cap MF\)
Trong mặt phẳng\((SAB)\) gọi \(R=SB\cap ME\)
Từ đó ta có thiết dện là \(MQPNR\).
b) Trong \((ABCD)\) gọi \(H=AC\cap NP\)
Trong \((SAC)\): gọi \(I=SO ∩ MH\)
Vậy \(I=SO\cap(MNP)\)
Bài 3 trang 77 sách giáo khoa hình học lớp 11
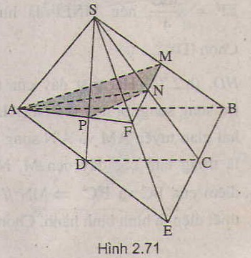
Cho hình chóp đỉnh \(S\) có đáy là hình thang \(ABCD\) với \(AB\) là đáy lớn. Gọi \(M, N\) theo thứ tự là trung điểm của các cạnh \(SB, SC\)
a) Tìm giao tuyến của hai mặt phẳng \((SAD)\) và \((SBC)\)
b) Tìm giao điểm của đường thẳng \(SD\) với mặt phẳng \((AMN)\)
c) Tìm thiết dện của hình chóp \(S.ABCD\) cắt bởi mặt phẳng \((AMN)\)
Lời giải:
a) Trong \((ABCD)\) gọi \(E=AD\cap BC\)
Do đó \((SAD) ∩ (SBC) = SE\)
b) Trong \((SBE)\): gọi \(F=MN ∩ SE\)
Trong \((SAE)\): gọi \(P= AF ∩ SD\)
Do đó \(P=SD\cap (AMN)\)
c) Thiết diện là tứ giác \(AMNP\).
Giaibaitap.me
Giải bài tập trang 78 bài ôn tập chương II - Đường thẳng và mặt phẳng trong không gian quan hệ song song Sách giáo khoa (SGK) Hình học 11. Câu 1: Tìm mệnh đề sai trong các mệnh đề sau đây...
Giải bài tập trang 79, 80 bài ôn tập chương II - Đường thẳng và mặt phẳng trong không gian quan hệ song song Sách giáo khoa (SGK) Hình học 11. Câu 4: Tìm mệnh đề đúng trong các mệnh đề sau:...
Giải bài tập trang 80 bài ôn tập chương II - Đường thẳng và mặt phẳng trong không gian quan hệ song song Sách giáo khoa (SGK) Hình học 11. Câu 9: Cho hình bình hành ABCD ...
Giải bài tập trang 91, 92 bài 1 vector trong không gian Sách giáo khoa (SGK) Hình học 11. Câu 1: Cho hình lăng trụ tứ giác...
