Bài 1 trang 91 sgk Hình học 11

Cho hình lăng trụ tứ giác: \(ABCD.A'B'C'D'\). Mặt phẳng \((P)\) cắt các cạnh bên \(AA', BB', CC', DD'\) lần lượt tại \(I, K, L, M\). xét các véctơ có các điểm đầu là các điểm \(I, K, L, M\) và có các điểm cuối là các đỉnh của hình lăng trụ. hãy chỉ ra các véctơ:

 a) Các véctơ cùng phương với \(\overrightarrow{IA}\);

b) Các véctơ cùng hướng với \(\overrightarrow{IA}\);

c) Các véctơ ngược hướng với \(\overrightarrow{IA}\).

Giải.

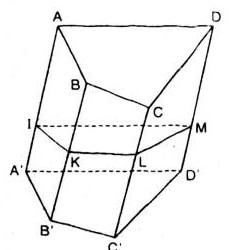
 a) Các véctơ cùng phương với \(\overrightarrow{IA}\) là: \(\overrightarrow{IA'}\), \(\overrightarrow{KB}\), \(\overrightarrow{KB'}\), \(\overrightarrow{LC}\), \(\overrightarrow{LC'}\), \(\overrightarrow{MD}\), \(\overrightarrow{MD'}\).

 b) Các véctơ cùng hướng với \(\overrightarrow{IA}\) là: \(\overrightarrow{KB}\), \(\overrightarrow{LC}\), \(\overrightarrow{MD}\).

 c) Các véctơ ngược hướng với \(\overrightarrow{IA}\) là: \(\overrightarrow{IA'}\), \(\overrightarrow{KB'}\), \(\overrightarrow{LC'}\), \(\overrightarrow{MD'}\).

Bài 2 trang 91 sgk hình học 11

Cho hình hộp \(ABCD.A'B'C'D'\). Chứng minh rằng:

a) \(\overrightarrow{AB}\) + \(\overrightarrow{B'C'}\) + \(\overrightarrow{DD'}\) = \(\overrightarrow{AC'}\);

b)  \(\overrightarrow{BD}\) - \(\overrightarrow{D'D}\) - \(\overrightarrow{B'D'}\) = \(\overrightarrow{BB'}\);

c)  \(\overrightarrow{AC}\) + \(\overrightarrow{BA'}\) + \(\overrightarrow{DB}\) + \(\overrightarrow{C'D}\) = \(\overrightarrow{0}\).

Giải

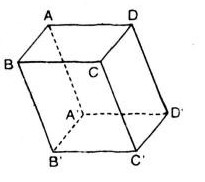
a) \(\overrightarrow{AB}\) + \(\overrightarrow{B'C'}\) + \(\overrightarrow{DD'}\)  = \(\overrightarrow{AB}\) + \(\overrightarrow{BC}\) + \(\overrightarrow{CC'}\) = \(\overrightarrow{AC'}\); 

b) \(\overrightarrow{BD}\) - \(\overrightarrow{D'D}\) - \(\overrightarrow{B'D'}\) = \(\overrightarrow{BD}\) + \(\overrightarrow{DD'}\) + \(\overrightarrow{D'B'}\) = \(\overrightarrow{BB'}\);

c) \(\overrightarrow{AC}\) + \(\overrightarrow{BA'}\) + \(\overrightarrow{DB}\) + \(\overrightarrow{C'D}\) = \(\overrightarrow{AC}\) + \(\overrightarrow{CD'}\) + \(\overrightarrow{D'B'}\) + \(\overrightarrow{B'A}\) = \(\overrightarrow{0}\).

Bài 3 trang 91 sgk hình học 11

 Cho hình bình hành \(ABCD\). Gọi \(S\) là một điểm nằm ngoài mặt phẳng chứa hình bình hành. chứng minh rằng: \(\overrightarrow{SA}\) + \(\overrightarrow{SC}\) = \(\overrightarrow{SB}\) + \(\overrightarrow{SD}\).

Giải

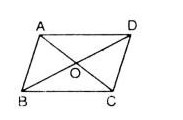
Gọi \(O\) là tâm của hình bình hành \(ABCD\). Khi đó: 

\(\left.\begin{matrix}\overrightarrow{SA} +\overrightarrow{SC}= 2\overrightarrow{SO}\\ \overrightarrow{SB}+\overrightarrow{SD}=2\overrightarrow{SO} \end{matrix}\right\}\Leftrightarrow \overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}.\)

Bài 4 trang 92 sgk hình học 11

Cho hình tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(CD\). Chứng minh rằng: 

a) \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right );\)

b) \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right ).\)

Giải

(Hình 33)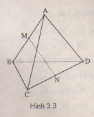 

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{DN}.\)

    \(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}.\) 

Cộng từng vế ta được: \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right )\)

b) 

\(\eqalign{
& \overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} \cr
& \overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DN} \cr} \)

Cộng từng vế ta được: \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right ).\)

Bài 5 trang 92 sgk hình học 11

Cho hình tứ diện \(ABCD\). Hãy xác định hai điểm \(E, F\) sao cho:

a) \(\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD};\)

b) \(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}.\)

Giải

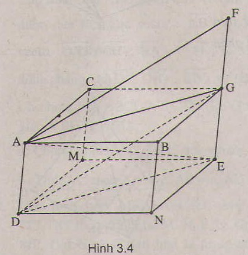
(H.3.4)

a) \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AG}\) với \(G\) là đỉnh của hình bình hành \(ABGC\). Ta có: 

\(\overrightarrow{AG}+\overrightarrow{AD}=\overrightarrow{AE}\Rightarrow\) \(E\) là đỉnh của hình bình hành \(ADEG\).

b) Ta có \(\overrightarrow{AG}-\overrightarrow{AD}=\overrightarrow{AF}\Rightarrow\) \(F\) là đỉnh của hình bình hành \(ADGF\).

Giaibaitap.me