Bài 1 trang 63 sách giáo khoa hình học lớp 11
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng.
a) Gọi \(O\) và \(O'\) lần lượt là tâm của các hình bình hành \(ABCD\) và \(ABEF\). Chứng minh rằng đường thằng \(OO'\) song song với các mặt phẳng \((ADF)\) và \((BCF)\)
b) Gọi \(M\) và \(N\) lần lượt là trọng tâm của hai tam giác \(ABD\) và \(ABE\). Chứng minh đường thẳng \(MN\) song song với mặt phẳng \((CEF)\)
Lời giải:
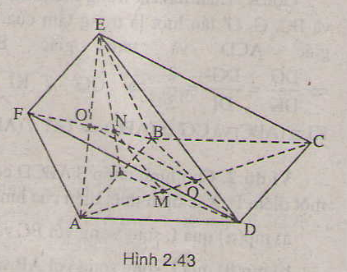
a) \(OO'\) là đường trung bình của tam giác \(DBF\) nên \(OO' // DF\).
\(DF\) nằm trong mặt phẳng \((ADF)\) nên \(OO' // mp(ADF)\).
Tương tự \(OO' // CE\) mà \(CE\) nằm trong mặt phẳng \((BCE)\) nên \(OO' // mp(BCE)\).
b) Gọi \(J\) là trung điểm đoạn thẳng \(AB\),
Ta có: \({{JM}\over{JD}}={{JN}\over{JE}}={1\over3}\Rightarrow MN//ED\)
\(ED\subset (CEF) \Rightarrow MN//(CEF)\)
Bài 2 trang 63 sách giáo khoa hình học lớp 11
Cho tứ diện \(ABCD\). Trên cạnh \(AB\) lấy một điểm \(M\). Cho \((α)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(AC\) và \(BD\)
a) Tìm giao tuyến của \((α)\) với các mặt tứ diện
b) Thiết diện của tứ diện cắt bởi mặt phẳng \((α)\) là hình gì?
Lời giải:
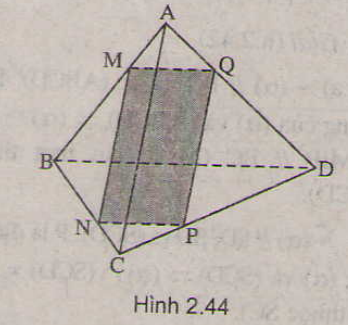
a) \((α) // AC, AC ∈(ABC), M\) là điểm chung của \(( α)\) và \((ABC)\) \(\Rightarrow (α) ∩ (ABC) = MN // AC\). Các giao tuyến sau tương tự.
b) Thiết diện là hình bình hành \(MNPQ\)
Bài 3 trang 63 sách giáo khoa hình học lớp 11
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một tứ giác lồi. Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\). Xác định thiết diện của hình chóp cắt bởi mặt phẳng \((α)\) đi qua \(O\), song song với \(AB\) và \(SC\). Thiết diện đó là hình gì?
Lời giải:
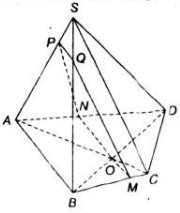
\((α) // AB, AB ⊂ (ABCD)\), \(O\) là điểm chung của \((α)\) và \((ABCD)\)
\(\Rightarrow ( α) ∩ (ABCD) = MN\) qua \(O\) và song song với \(AB\).
Các giao tuyến khác tương tự: \(MQ//SC\), \(QP //AB\).
Thiết diện là hình thang \(MNPQ\).
Giaibaitap.me
Giải bài tập trang 71 bài 4 hai mặt phẳng song song Sách giáo khoa (SGK) Hình học 11. Câu 1: Hãy xác định giao điểm...
Giải bài tập trang 77 bài ôn tập chương II - Đường thẳng và mặt phẳng trong không gian quan hệ song song Sách giáo khoa (SGK) Hình học 11. Câu 1: Tìm giao tuyến của các mặt phắng sau...
Giải bài tập trang 78 bài ôn tập chương II - Đường thẳng và mặt phẳng trong không gian quan hệ song song Sách giáo khoa (SGK) Hình học 11. Câu 1: Tìm mệnh đề sai trong các mệnh đề sau đây...
Giải bài tập trang 79, 80 bài ôn tập chương II - Đường thẳng và mặt phẳng trong không gian quan hệ song song Sách giáo khoa (SGK) Hình học 11. Câu 4: Tìm mệnh đề đúng trong các mệnh đề sau:...
