Bài 1 trang 23 sách giáo khoa hình học lớp 11

Trong mặt phẳng \(Oxy\) cho các điểm \(A(-3;2), B(-4;5)\) và \(C(-1;3)\)

a) Chứng minh rằng các điểm \(A'(2;3), B'(5;4)\) và \(C'(3;1)\) theo thứ tự là ảnh của \(A, B\) và \(C\) qua phép quay tâm \(O\) góc -\( 90^{\circ}\).

b) Gọi tam giác \({A_{1}}\)\({B_{1}}\)\({C_{1}}\) là ảnh của tam giác \(ABC\) qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm \(O\) góc - \( 90^{\circ}\) và phép đối xứng qua trục \(Ox\). Tìm tọa độ các đỉnh của tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\)

Lời giải:

a) (hình bên) 

Gọi \(r = OA, α\) là góc lượng giác \((Ox, OA)\), \(β\) là góc lượng giác \((Ox, OA')\). Giả sử \(A'= ( x'; y')\). Khi đó ta có:

\(β = α - \)\( 90^{\circ}\), \(x = r cos α, y = r sin α\)

Suy ra

\(x' = r cos β = r cos ( α -\) \( 90^{\circ}\))\( = r sinα = y\)

\(y' = r sin β = r sin ( α -\) \( 90^{\circ}\)) \(= - r cos α= - x\)

Do đó phép quay tâm \(O\) góc - \( 90^{\circ}\) biến \(A(-3;2)\) thành \(A'(2;3)\). Các trường hợp khác làm tương tự

b) ( hình 1.26)

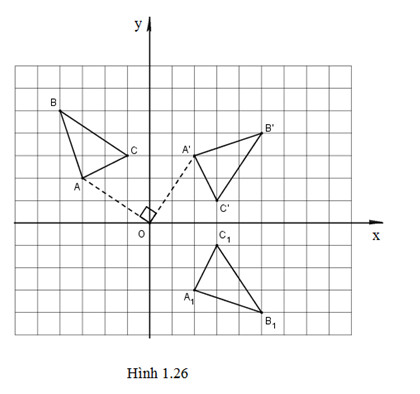
Gọi tam giác \({A_{1}}^{}\)\({B_{1}}^{}\)\({C_{1}}^{}\) là ảnh của tam giác \(A'B'C'\) qua phép đối xứng trục \(Ox\). Khi đó \({A_{1}}^{}\)(2;-3), \({B_{1}}^{}\) (5;-4), \({C_{1}}^{}\)(3;-1) là đáp số cần tìm.

Bài 2 trang 24 sách giáo khoa hình học 11

Cho hình chữ nhật \(ABCD\). Gọi \(E, F, H, K, O, I, J\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DA, KF, HC, KO\). Chứng minh hai hình thang\(AEJK\) và \(FOIC\) bằng nhau.

Lời giải:

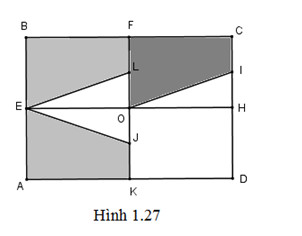
Gọi \(L\) là trung điểm của đoạn thẳng \(OF\). Ta thấy phép đối xứng qua đường thẳng \(EH\) biến hình thang \(AEJK\) thành hình thang \(BELF\), phép tịnh tiến theo vectơ \(BF\) biến hình thang \(BELF\) thành hình thang \(FOIC\). Như vậy phép dời hình có được bằng cách thực hiện liên tiếp phép biến hình trên, sẽ biến hình thang \(AEJK\) thành hình thang \(FOIC\). Do đó hai hình thang \(AEJK\) và \(FOIC\) bằng nhau.

Bài 3 trang 24 sách giáo khoa hình học 11

 Chứng minh rằng: Nếu một phép dời hình biến tam giác \(ABC\) thành tam giác \(A'B'C'\) thì nó cũng biến trọng tâm của tam giác \(ABC\) tương ứng thành trọng tâm của tam giác \(A'B'C'\)

Lời giải:

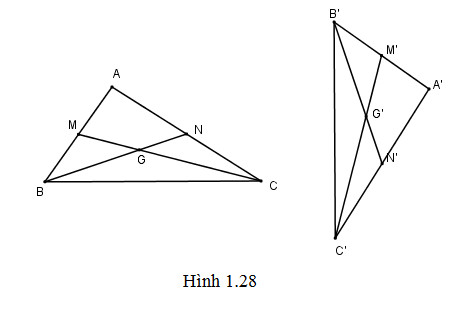
Gọi phép dời hình đó là \(f\). Do \(f\) biến các đoạn thẳng \(AB, AC\) tương ứng thành các đoạn thẳng \(A'B', A'C' \) nên nó cũng biến các trung điểm \(M, N\) của các đoạn thẳng \(AB, AC\) tương ứng theo thứ tự thành các trung điểm \(M', N'\) của các đoạn thẳng \(A'B', A'C'\). Vậy \(f\) biến các trung tuyến \(CM, BN\) của tam giác \(ABC\) tương ứng thành các trung tuyến \(C'M', B'N'\) của tam giác \(A'B'C'\). Từ đó suy ra \(f\) biến trọng tâm \(G\) của tam giác \(ABC\) của \(CM\) và \(BN\) thành trọng tâm \(G'\) của tam giác \(A'B'C'\) là giao của \(C'M'\) và \(B'N'\).

Giaibaitap.me