Bài 1 trang 34 sách giáo khoa hình học lớp 11

Cho lục giác đều \(ABCDEF\) tâm \(O\). Tìm ảnh của tam giác \(AOF\).

a) Qua phép tịnh tiến theo vectơ \(AB\)

b) Qua phép đối xứng qua đường thẳng \(BE\)

c) Qua phép quay tâm \(O\) góc \( 120^{\circ}\)

Lời giải:

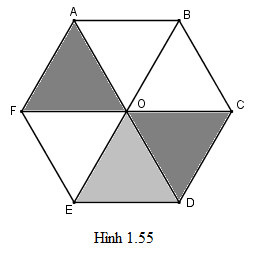
a) Tam giác \(BCO\)

b) Tam giác \(COD\)

c) Tam giác \(EOD\)

Bài 2 trang 34 sách giáo khoa hình học lớp 11

Trong mặt phẳng tọa độ \(Oxy\) cho điểm \(A(-1;2)\) và đường thẳng \(d\) có phương trình \(3x + y+ 1= 0\). Tìm ảnh của \(A\) và \(d\)

a) Qua phép tịnh tiến theo vectơ \(v = (2;1)\)

b) Qua phép đối xứng qua trục \(Oy\)

c) Qua phép đối xứng qua gốc tọa độ

d) Qua phép quay tâm \(O\) góc \( 90^{\circ}\)

Lời giải:

Gọi \(A'\) và \(d'\) theo thứ tự là ảnh của \(A\) và \(d\) qua phép biến hình trên

a) \(A' = (-1+2; 2+1) = (1;3)\), \(d // d'\), nên d có phương trình : \(3x +y + C = 0\). Vì \(A\) thuộc \(d\), nên \(A'\) thuộc \(d'\), do đó \(3.1 +3 + C = 0\). Suy ra \(C=-6\). Do đó phương trình của \(d'\) là \(3x+y-6=0\)

b) \(A (-1;2)\) và \(B(0;-1)\) thuộc \(d\). Ảnh của \(A\) và \(B\) qua phép đối xứng qua trục \(Oy\) tương ứng là \(A'(1;2)\) và \(B'(0;-1)\). Vậy \(d'\) là đường thẳng \(A'B'\) có phương trình :

\( \frac{x- 1}{-1}\) =  \( \frac{y-2}{-3}\)

 hay \(3x - y - 1 =0\)

c) \(A'=( 1;-2) , d'\) có phương trình \(3x + y -1 =0\)

d) Qua phép quay tâm \(O\) góc \( 90^{\circ}\), \(A\) biến thành \(A'( -2; -1), B\) biến thành \(B'(1;0)\). Vậy \(d'\) là đường thẳng \(A'B'\) có phương trình

\( \frac{x-1}{-3}\) = \( \frac{y}{-1}\)

 hay \(x- 3y - 1 = 0\)

Bài 3 trang 34 sách giáo khoa hình học lớp 11

Trong mặt phẳng tọa độ \(Oxy\), cho đường tròn tâm \(I(3;-2)\), bán kính \(3\)

a) Viết phương trình của đường tròn đó

b) Viết phương trình ảnh của đường tròn \((I;3)\) qua phép tịnh tiến theo vectơ \(v = (-2;1)\)

c) Viết phương trình ảnh của đường tròn \((I;3)\) qua phép đối xứng qua trục \(Ox\)

d) Viết phương trình ảnh của đường tròn \((I;3)\) qua phép đối xứng qua gốc tọa độ

Lời giải:

Gọi \(I'\) là ảnh của \(I\) qua phép biến hình nói trên

a) Phương trình của đường tròn \((I;3)\) là:

\((x-3)^{2}\) + \((y+2)^{2} = 9\)

b) \({T_{\overrightarrow{v}}} (I) = I' (1;-1)\), phương trình đường tròn ảnh : \((x-1)^{2}+(y+1)^{2}=9\)

c) \({D_{Ox}} (I) = I'(3;2)\), phương trình đường tròn ảnh: \((x-3)^{2}+(y-2)^{2}=9\)

d) \({D_{O}}(I) = I'( -3;2)\), phương trình đường tròn ảnh: \((x+3)^{2}+(y-2)^{2}=9\)

Bài 4 trang 34 sách giáo khoa hình học lớp 11

Cho vectơ \(v\), đường thẳng \(d\) vuông góc với giá của vectơ \(v\). Gọi \(d'\) là ảnh của \(d\) qua phép tịnh tiến theo vectơ \( \frac{1}{2}\) \( \overrightarrow{v}\). Chứng minh rằng phép tịnh tiến theo vectơ \( \overrightarrow{v}\)

Lời giải:

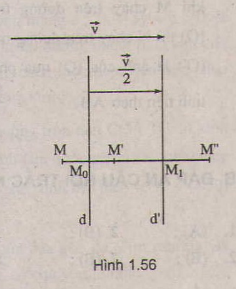
Lấy \(M\) tùy ý. Gọi \({D_{d}}(M) = M'\), \({D_{d'}} (M') = M''\).

Gọi \(M_0,M_1\) lần lượt là giao của \(d\) và \(d'\) với \(MM''\)

Ta có

\( \overrightarrow{MM''}\) =\(\overrightarrow{MM'} + \overrightarrow{M'M''}= 2\overrightarrow{{M_{0}M'}^{}} + 2 \overrightarrow{M'{M_{1}}^{}}\)

\(= 2 \overrightarrow{{M_{0}{M_{1}}^{}}^{}} = 2 \frac{\overrightarrow{v}}{2} = \overrightarrow{v}\)

Vậy \(M'' = {T_{\overrightarrow{v}}} (M) = {D_{d'}}\) \({D_{d}}(M)\), với mọi \(M\)

Do đó phép tịnh tiến theo vectơ \(v\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).