Bài 1 trang 97 sgk toán 11

Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó:

a) \(u_n= 5 - 2n\);                         b) \(u_n=  \frac{n}{2}- 1\);

c) \(u_n= 3^n\)           ;                      d) \(u_n=  \frac{7-3n}{2}\)

Bài 2 trang 97 sgk toán 11

Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:

a) \( \left\{\begin{matrix} u_{1}-u_{3}+u_{5}=10\\ u_{1}+u_{6=17} \end{matrix}\right.\),                        

b) \( \left\{\begin{matrix} u_{7}-u_{3}=8\\ u_{2}.u_{7}=75 \end{matrix}\right.\).

Hướng dẫn giải:

Sử dụng công thức \(u_n= u_1+ (n – 1)d\).

a) Từ hệ thức đã cho ta có:

\( \left\{\begin{matrix} u_{1}-u_{1}-2d+u_{1}+4d=10\\ u_{1}+u_{1}+5d =17 \end{matrix}\right.\) hay \( \left\{\begin{matrix} u_{1}+2d=10\\ 2u_{1}+5d = 17 \end{matrix}\right.\)

.Giải hệ ta được: \(u_1= 16, d = -3\).

b) Từ hệ đã cho ta có:

\( \left\{\begin{matrix} u_{1}+6d-u_{1}-2d =8\\ (u_{1}+d)(u_{1}+6d)=75 \end{matrix}\right.\)  hay \( \left\{\begin{matrix} 2d =4\\ (u_{1}+d)(u_{1}+6d)=75 \end{matrix}\right.\)

Giải hệ ta được:  \(u_1= 3\) và \(d = 2\) hoặc \(u_1= -17\) và \(d = 2\)

Bài 3 trang 97 sgk toán 11

 Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng \(u_1, n, d, u_n, S_n\).

a) Hãy viết các hệ thức liên hệ giữa các đại lượng để có thể tìm được các đại lượng còn lại?

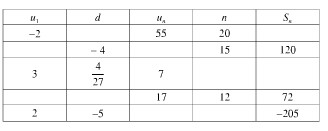
b) Lập bảng theo mẫu sau và điền vào chỗ trống thích hợp:

Hướng dẫn giải:

a) Cần biết ít nhất ba trong năm đại lượng \(u_1, n, d, u_n, S_n\) thì có thể tính được hai đại lượng còn lại.

b) Thực chất đây là năm bài tập nhỏ, mỗi bài ứng với các dữ liệu ở một dòng. Học sinh phải giải từng bài nhỏ rồi mới điền kết quả.

b1) Biết \(u_1= -2, u_n= 55, n = 20\). Tìm \(d, S_n\)   

Áp dụng công thức \(d = {{{u_n} - {u_1}} \over {n - 1}},{S_n} = {{({u_1} + {u_n}).n} \over 2}\)

Đáp số: \(d = 3, S_{20}= 530\).

b2) Biết \(d = -4, n = 15\), \(S_n= 120\). Tìm \(u_1,u_n\)

Áp dụng công thức \(u_n= u_1+ (n - 1)d\) và \({S_n} = {{({u_1} + {u_n}).n} \over 2}\)

ta có: 

\(\left\{ \matrix{
{u_1} - {u_{15}} = 56 \hfill \cr
{u_1} + {u_{15}} = 16 \hfill \cr} \right.\)

Giải hệ trên, ta được \(u_1= 36, u_{15}= - 20\).

b3) Áp dụng công thức \(u_n= u_1+ (n - 1)d\), từ đây ta tìm được \(n\); tiếp theo áp dụng công thức \({S_n} = {{({u_1} + {u_n}).n} \over 2}\). Đáp số: \(n = 28\), \(S_n= 140\).

b4) Áp dụng công thức \({S_n} = {{({u_1} + {u_n}).n} \over 2}\), từ đây tìm được \(u_1\), tiếp theo áp dụng công thức \(u_n= u_1+ (n - 1)d\) để tìm \(d\). Đáp số: \(u_1= -5, d= 2\).

b5) Áp dụng công thức \({S_n} = {{\left[ {2{u_1} + (n - 1)d} \right].n} \over 2}\), từ đây tìm được \(n\), tiếp theo áp dụng công thức \(u_n= u_1+ (n - 1)d\). Đáp số: \(n = 10, u_n= -43\).

Bài 4 trang 98 sgk toán 11

 Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân \(0,5 m\). Cầu thang đi từ tầng một lên tầng \(2\) gồm \(21\) bậc, mỗi bậc cao \(18 cm\).

a) Hãy viết công thức để tìm độ cao của một bậc tuỳ ý so với mặt sân.

b) Tính độ cao của sàn tầng hai so với mặt sân.

Hướng dẫn giải:

a) Gọi chiều cao của bậc thứ \(n\) so với mặt sân là \(h_n\)

Ta có:         \( h_n= 0,5 + n.0,18(m)\).

b) Chiều cao mặt sàn tầng hai so với mặt sân là

                    \(h_{21}= 0,5 + 21.0,18 = 4,28 (m)\).

Bài 5 trang 98 sgk toán 11

Từ \(0\) giờ đến \(12\) giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ

Hướng dẫn giải:

Đồng hồ đánh số tiếng chuông là: \(S = 1 + 2 + 3 +....+ 12\). Đây là tổng của \(12\) số hạng của cấp số cộng có \(u_1= 1, u_{12}= 12\). Do đó áp dụng công thức tính tổng,

ta có \(S =  \frac{(1+12).12}{2} = 78\).

Vậy đồng hồ đánh \(78\) tiếng chuông.

Giaibaitap.me