Bài 5 trang 114 sgk Hình học 11

Cho hình lập phương \(ABCD.A'B'C'D'\). Chứng minh rằng:

a) Mặt phẳng \((AB'C'D)\) vuông góc với mặt phẳng \((BCD'A')\);

b) Đường thẳng \(AC'\) vuông góc với mặt phẳng \((A'BD)\).

Giải

(H.3.45)

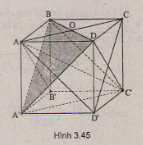
a) \(BC ⊥ (ABB'A') \Rightarrow BC ⊥ AB'\);

Mà \(BA' ⊥ AB'  \Rightarrow AB' ⊥ (BCD'A')\).

Ta có \(AB' ⊂ (AB'C'D)\) nên (\(AB'C'D) ⊥ (BCD'A')\).

b)  +) \(AA'\bot(ABCD) \Rightarrow AA'\bot BD\)

Mà  \(BD\bot AC\Rightarrow BD\bot (ACC'A')\)

\(AC'\subset(ACC'A')\) nên suy ra \(BD\bot AC'\)    (1)

  +) \(AB\bot (ADD'A')\Rightarrow AB\bot A'D \)

Mà \(AD'\bot  A'D\Rightarrow  A'D\bot (ABC'D')\)

Ta có \(AC'\subset (ABC'D')\Rightarrow AC'\bot A'D\)      (2)

Từ (1) và (2) suy ra: \(AC' ⊥ (A'BD)\).

Bài 6 trang 114 sgk Hình học 11

 Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình thoi cạnh \(a\) và có \(SA = SB = SC = a\). Chứng minh rằng:

a) Mặt phẳng \((ABCD)\) vuông góc với mặt phẳng \((SBD)\);

b) Tam giác \(SBD\) là tam giác vuông.

Giải

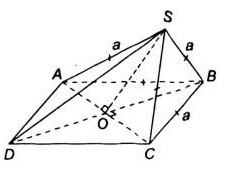
a) Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\)

Theo tính chất của hình thoi thì \(O\) là trung điểm của \(AC,BD\)

Xét tam giác cân \(SAC\) cân tại \(S\) có \(SO\) vừa là đường trung tuyến đồng thời là đường cao do đó 

\(SO\bot AC\)                                                             (1)

Mặt khác \(ABCD\) là hình thoi nên \(AC\bot BD\)      (2)

Từ (1) và (2) suy ra \(AC\bot (SBD)\)

\(AC\subset (ABCD)\Rightarrow (ABCD)\bot (SBD)\)

b) \(∆SAC = ∆BAC  (c.c.c)\)

Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau: \(SO = BO\)

\(O\) là trung điểm của \(BD\) nên \(OB=OD\)

Suy ra \(SO=OB=OD={1\over 2} BD\)

Đường trung tuyến ứng với một cạnh của tam giác và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông. Do đó tam giác \(SBD\) vuông tại \(S\)

Bài 7 trang 114 sgk hình học 11

 Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a, BC = b, CC' = c\).

a) Chứng minh rằng mặt phẳng \((ADC'B')\) vuông góc với mặt phẳng \((ABB'A')\).

b) Tính độ dài đường chéo \(AC'\) theo \(a, b, c\).

Giải

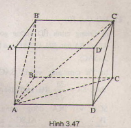
a) Ta có: \(DA ⊥ (ABB'A'), DA ⊂ (ADC'B')\)

\(\Rightarrow (ADC'B') \bot(ABB'A')\).

b) Xét tam giác vuông \(ACC'\)) 

 \(AC' = \sqrt {A{C^2} + CC{'^2}}  = \sqrt {A{D^2} + D{C^2} + CC{'^2}}\)

          \(=\sqrt{a^{2}+b^{2}+c^{2}}.\)

Ghi nhớ: Hai mặt phẳng vuông góc với nhau khi mặt này chứa một đường thẳng vuông góc với mặt kia.

Bài 8 trang 114 SGK Hình học 11

Tính độ dài đường chéo của một hình lập phương cạnh \(a\).

Giải

Hình hộp chữ nhật có độ dài đường chéo là: \(AC' = \sqrt {{a^2} + {b^2} + {c^2}} \)

Hình lập phương là hình hộp chữ nhật có \(a=b=c\) nên ta có đường chéo \(AC'=\sqrt {{a^2} + {a^2} + {a^2}} =\sqrt {3{a^2}}  = a\sqrt 3\)

Giaibaitap.me