Bài 1 trang 46 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

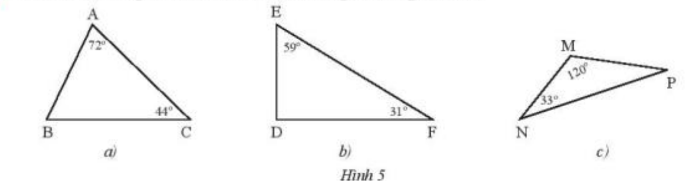
Lời giải:

a) Theo định lí về tổng số đo 3 góc trong tam giác ta có :

\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B = {180^o} - \widehat A - \widehat C = {180^o} - {72^o} - {44^o} = {64^o}\end{array}\)

b) Theo định lí về tổng số đo 3 góc trong tam giác ta có :

\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow \widehat D = {180^o} - \widehat E - \widehat F = {180^o} - {59^o} - {31^o} = {90^o}\end{array}\)

c) Theo định lí về tổng số đo 3 góc trong tam giác ta có :

\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {120^o} - {33^o} = {27^o}\end{array}\) 

Bài 2 trang 47 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Tính số đo x của góc trong Hình 6.

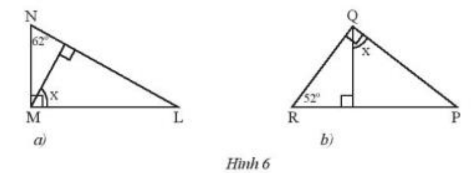
Lời giải: 

a) Gọi MP vuông góc với NL (P thuộc NL)

Vì tam giác MNL vuông tại M nên ta có

\( \Rightarrow \widehat L = {90^o} - \widehat N = {28^o}\)

Xét tam giác MPL vuông tại P nên ta có :

\( \Rightarrow \widehat x = {90^o} - \widehat L = {90^o} - {28^o} = {62^o}\)

b) Gọi QF vuông góc với RP (F thuộc RP)

Vì tam giác RQP vuông tại Q nên ta có :

\( \Rightarrow \widehat R + \widehat P = {90^o} \Rightarrow \widehat P = {90^o} - {52^o} = {38^o}\)

Vì tam giác QFP vuông tại F \( \Rightarrow \widehat x + \widehat P = {90^o} \Rightarrow \widehat x = {90^o} - {38^o} = {52^o}\) 

Bài 3 trang 47 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc \(\widehat A\),\(\widehat B\),\(\widehat C\),\(\widehat D\).

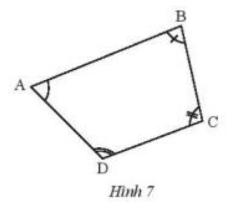
Lời giải: 

Ta chia tứ giác ABCD thành tam giác ACD và tam giác ABC

\( \Rightarrow \) Số đo tổng các góc tam giác ACD = tổng số đo các góc tam giác ABC  = \({180^o}\)

\( \Rightarrow \)Tổng số đo các góc trong tứ giác ABCD = tổng số đo các góc 2 tam giác ACD và ABC \( = {2.180^o} = {360^o}\) 

Bài 4 trang 47 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?

a) 4cm; 5cm; 7cm

b) 2cm; 4cm; 6cm

c) 3cm; 4cm; 8cm

Lời giải:

Theo bất đẳng thức tam giác:

a) Ta xét :

4 + 5 > 7

4 + 7 > 5

5 + 7 > 4

\( \Rightarrow \) Cả 3 cạnh của tam giác đều thỏa mãn bất đẳng thức tam giác

\( \Rightarrow \) a là tam giác

b) Ta xét :

2 + 4 = 6

\( \Rightarrow \)  Cả 3 cạnh của tam giác không thỏa mãn bất đẳng thức tam giác

\( \Rightarrow \) b không là tam giác

c) Ta xét :

3 + 4 < 8

\( \Rightarrow \) Cả 3 cạnh của tam giác không thỏa mãn bất đẳng thức tam giác

\( \Rightarrow \) c không là tam giác 

Bài 5 trang 47 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Cho tam giác ABC có BC = 1cm, AB = 4cm. Tìm độ dài cạnh AC, biết rằng độ dài này là một số nguyên xăngtimét.

Lời giải: 

Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:

4– 1 < CA < 4 + 1

3 < CA < 5

Mà CA là số nguyên

 CA = 4 cm.

Vậy CA = 4 cm.

Bài 6 trang 47 sách giáo khoa Toán 7 Chân trời sáng tạo tập 2

Trong một trường học, người ta bắt đầu đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết các khoảng cách AC = 15m, AB = 45m

a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30m thì tại khu vực B có nhận được tín hiệu không? Vì sao?

b) Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60m.

Lời giải:

Áp dụng bất đẳng thức tam giác cho tam giác ABC ta có :

AB - AC < BC < AB + AC

45 - 15 < BC < 45 + 15

Vậy 30 m < BC < 60 m

a) Vì BC > 30 m nên trong phạm vi 30m, khu vực B không nhận được tín hiệu

b) Vì BC < 60 m nên trong phạm vi 60m, khu vực B nhận được tín hiệu.

Giaibaitap.me